Свойства ограниченности, замкнутости и выпуклости множеств

Решение оптимизационной задачи существенно зависит от вида области допустимых значений целевой функции. Область определения функции одной переменной есть некоторая область числовой прямой, двух переменных - плоскости, в общем случае – n -мерного пространства 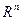. Познакомимся на уровне простых геометрических иллюстраций с понятиями ограниченности, замкнутости и выпуклости множеств в пространстве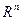

ПРИМЕР 3. Построить e–окрестность точки 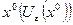и шар радиуса e с центром в точке 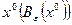при

а) , ;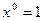

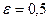b) , .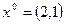

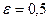► e–окрестностью точки 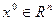называется множество точек пространства 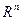, расстояние от которых до 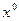меньше e. Поэтому в пространствах 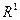, 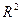данные множества можно изобразить следующим образом:

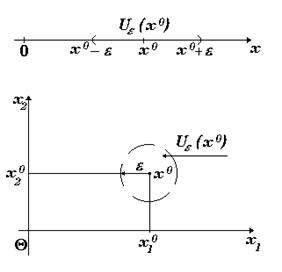
Рис. 2. Изображение e–окрестности на прямой и на плоскости.

a) 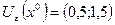, e–окрестность в 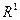- открытый промежуток;

b) .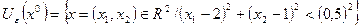

Заметим, что в обоих случаях граница 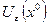, то есть множество точек соответствующего пространства, расстояние от которых до 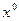равно e, не входит в e–окрестность. Если же мы дополним 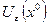такими точками, то получим шар радиуса e с центром в точке 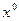. В нашем примере шарами будут, соответственно, отрезок 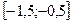и круг радиуса 0,5 с центром в точке . ◄

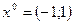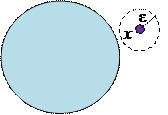
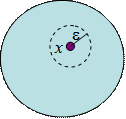
Внутренняя точка содержится в области вместе с некоторой окрестностью.

Внешняя точка содержится вне области вместе с некоторой окрестностью.

Граничная точка – такая точка, у которой любая окрестность содержит точки, как лежащие в области, так и не лежащие в области.

			Рис.5. Граничная точка

Открытое множество состоит только из внутренних точек (например: ).

Замкнутое множество содержит все свои граничные точки (например, круг или шар).

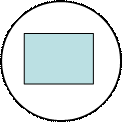
Область называется ограниченной, если вся она помещается в некоторый шар, и неограниченной, если не существует шара, вмещающего область целиком.

Область выпукла, если отрезок, соединяющий любые две точки из P, полностью принадлежит этому множеству. (Нет вмятин и дыр!)

Область невыпуклая, если есть отрезок, соединяющий две её точки, который содержит точки, не принадлежащие данной области Н

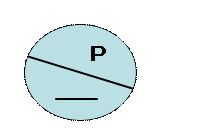
Рис.10. Выпуклая фигура Рис.11. Невыпуклая фигура

ПРИМЕР 4. Изобразить графически множество точек на плоскости и установить, обладает ли оно свойствами замкнутости, ограниченности, выпуклости.

a) .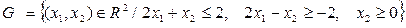

► Построим все три полуплоскости, задающие множество G (Подробно процесс построения полуплоскостей описан в примере 16). Искомое множество G есть пересечение, т.е. общая часть трех полуплоскостей (треугольная область ABC на рис.12).

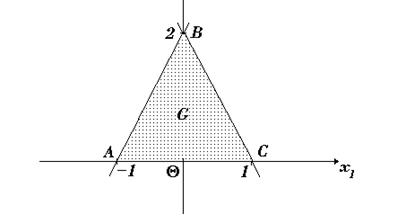
Рис.12.

Легко видеть, что множество G: замкнуто, т.к. содержит свою границу;

ограничено, т.к. его можно поместить в некоторый шар (например, в круг, описанный около треугольника ABC, или круг с центром в точке Q радиуса 2);

выпукло, т.к. является пересечением выпуклых множеств. ◄

b)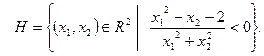

► Множество H есть множество точек, координаты которых удовлетворяют неравенству .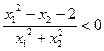

Левая часть неравенства определена во всех точках плоскости, за исключением Q(0,0), и во всех этих точках знак дроби совпадает со знаком ее числителя. Таким образом, множество H есть множество точек, координаты которых удовлетворяют неравенству 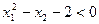(за исключением точки Q).

Построим множество H. Оно совпадает с одной из двух частей, на которые парабола 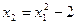делит плоскость. Подставляя в неравенство 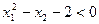координаты точки Q, получаем верное числовое неравенство 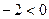. Это означает, что H – та из частей, которая содержит начало координат. Исключая из построенного множества точку Q, получаем искомое множество H.

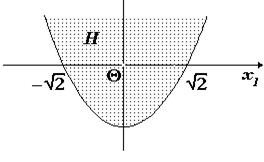
Рис.13.

Легко видеть, что множество H: неограничено; открыто: поскольку граница множества (парабола 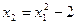) ему не принадлежит, все точки множества H являются внутренними точками этого множества. Оно не является выпуклым. Действительно, любой отрезок, соединяющий две точки множества H и проходящий через начало координат, содержит точку Q, не принадлежащую множеству H. ◄