Производной функции f(x) в точке х0 называется предел отношения приращения функции 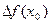 в точке х0 к приращению аргумента
в точке х0 к приращению аргумента 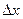 , когда приращение аргумента стремится к нулю.
, когда приращение аргумента стремится к нулю.
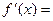 lim
lim 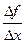 = lim
= lim 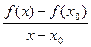
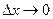
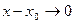
Правила дифференцирования 1. Производная суммы (разности) функций равна сумме (разности) производных:. 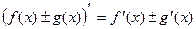 или или 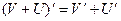 2. Постоянный множитель можно выносить за знак производной: 2. Постоянный множитель можно выносить за знак производной: 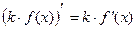 . 3. Производная произведения двух функций равна: . 3. Производная произведения двух функций равна: 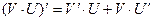 4. Производная частного двух функций равна: 4. Производная частного двух функций равна: 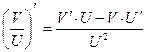 Пример: Пример: 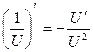 5. Производная сложной функции равна произведению производной внешней функции на производную ее аргумента. 5. Производная сложной функции равна произведению производной внешней функции на производную ее аргумента. 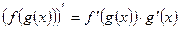 | ТАБЛИЦА ПРОИЗВОДНЫХ Постоянная 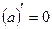  Линейная Линейная 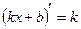 Степенная функция Степенная функция 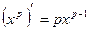 Показательная функция Показательная функция 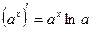 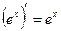 Логарифмическая функция Логарифмическая функция 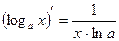 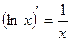 Тригонометрические функции Тригонометрические функции 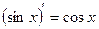 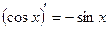 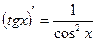 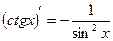 Обратные тригонометрические функции Обратные тригонометрические функции 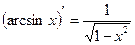 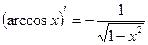 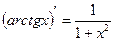 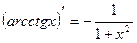 |
Дифференцирование степенных функций:
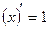
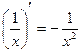
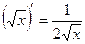
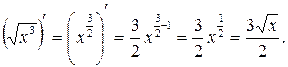
Пример. Найти производные функций:
а) 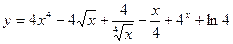
используем правило вычисления алгебраической суммы функций: производная суммы (разности) функций равна сумме (разности) производных: 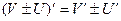 ,
,
затем вычислим каждое слагаемое отдельно, по правилу вычисления производной степенной функции: 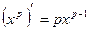 и, учитывая, что постоянный множитель можно выносить за знак производной:
и, учитывая, что постоянный множитель можно выносить за знак производной: 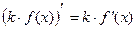
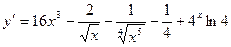
b) 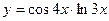
используем правило вычисления производной произведения двух функций: 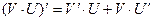
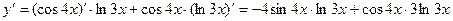
 2015-05-13
2015-05-13 1934
1934
