Замечание. Широко используемые в проективной геометрии однородные координаты позволяют эффективно описывать так называемые несобственные элементы (по существу те

Широко используемые в проективной геометрии однородные координаты позволяют эффективно описывать так называемые несобственные элементы (по существу те, которыми проективная плоскость отличается от привычной нам евклидовой плоскости). Более подробно о новых возможностях, предоставляемых введенными однородными координатами, говорится в четвертом разделе этой главы.

В проективной геометрии для однородных координат, принято следующее обозначение:

х: у: 1, или, более обще, x₁: х₂: х₃

(напомним, что здесь непременно требуется, чтобы числа х₁, х₂, х₃ одновременно, в нуль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения h (например, h = 1) точку с однородными координатами

(0.5 0.1 2.5)

представить нельзя. Однако при разумном выборе h можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при h = 10 для рассматриваемого примера имеем

(5, 1, 25).

Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами (80000 40000 1000) можно взять, например, h=0,001. В результате получим (80 40 1).

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

В самом деле, считая h = 1, сравним две записи: помеченную символом * и нижеследующую, матричную:

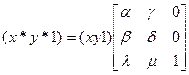
Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство 1=1.

Тем самым сравниваемые записи можно считать равносильными.