Постановка задачи. Найти координаты точки 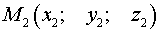 , симметричной точке
, симметричной точке 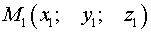 относительно плоскости
относительно плоскости 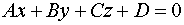 .
.
План решения.
1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку 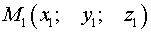 . Так прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е.
. Так прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е.
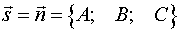 .
.
Поэтому уравнение прямой будет
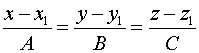 .
.
2. Находим точку 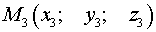 пересечения прямой
пересечения прямой 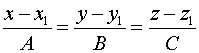 и плоскости
и плоскости 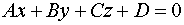 (см. задачу 13).
(см. задачу 13).
3. Точка 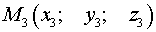 является серединой отрезка
является серединой отрезка 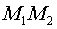 , где точка
, где точка 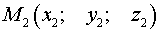 является точкой симметричной точке
является точкой симметричной точке 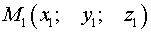 , поэтому
, поэтому
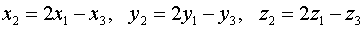 .
.
Задача 14. Найти точку 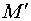 , симметричную точке
, симметричную точке 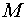 относительно плоскости.
относительно плоскости.
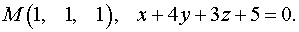
Уравнение прямой, которая проходит через точку 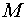 перпендикулярно заданной плоскости будет:
перпендикулярно заданной плоскости будет:
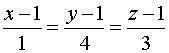 .
.
Найдем точку пересечения прямой и плоскости.
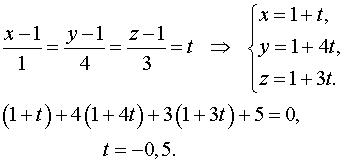
Откуда 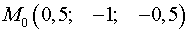 – точка пересечения прямой и плоскости.
– точка пересечения прямой и плоскости. 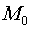 является серединой отрезка
является серединой отрезка 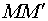 , поэтому
, поэтому
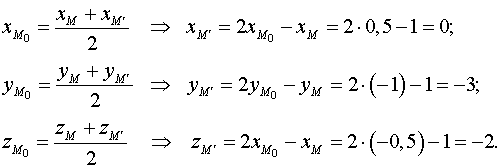
Т.е. 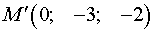 .
.
 2015-05-30
2015-05-30 45712
45712
