Некоторые ориентации трехмерного объекта нельзя получить одними вращениями, требуются преобразования отражения. В трехмерном пространстве отражение происходит относительно плоскости. По аналогии с двумерным отражением, трехмерное отражение относительно плоскости эквивалентно вращению вокруг оси в трехмерном пространстве в четырехмерное и обратно в исходное трехмерное пространство. Для чистого отражения детерминант матрицы равен -1.
В общем случае матрица отражения имеет следующий вид:
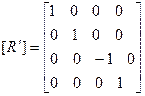 - отражение относительно плоскости xy.
- отражение относительно плоскости xy.
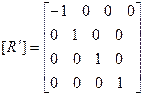 - отражение относительно плоскости yz.
- отражение относительно плоскости yz.
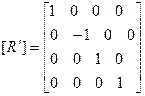 - отражение относительно плоскости xz.
- отражение относительно плоскости xz.
Симметрии относительно плоскостей 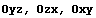 , осей
, осей 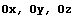 и точки
и точки 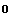 (начала координат) задаются матрицами
(начала координат) задаются матрицами
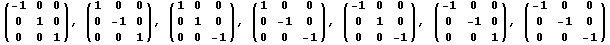
Симметрии относительно произвольных плоскостей и прямых можно получить по той же формуле, что и растяжения, взяв в качестве 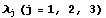 нужную комбинацию чисел
нужную комбинацию чисел 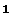 и
и 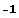 . Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы
. Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы 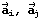 , для которых
, для которых 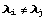 , должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно
, должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно 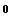 :
: 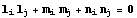 .
.
При отыскании нужных векторов полезно иметь в виду, что вектор с координатами 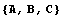 перпендикулярен плоскости
перпендикулярен плоскости 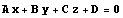 .
.
В частности, матрица симметрии относительно плоскости 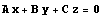 имеет вид
имеет вид
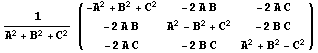
 2015-05-30
2015-05-30 7016
7016
