Моделирование процесса принятия решений по управлению проектами в нечетких условиях

М.А. Беляева

При управлении проектами возникает необходимость принятия решений по широкому кругу слабоструктурированных задач в условиях неопределенности и нечеткости. Традиционным подходом в управлении проектом в условиях неопределенности является вероятностный подход. Однако зачастую неизвестны функции распределения различных параметров проекта, требуется определение качественных характеристик проекта, решение слабоформализованных и слабоструктурированных задач, что методы теории вероятностей не позволяют осуществлять. Применение теории вероятности для оперирования с неопределенными величинами и параметрами проекта, приводит к тому, что неопределенность, возникающая при управлении проектами независимо от ее природы, отождествляется со случайностью, тогда как основным источником неопределенности в управлении проектами является нечеткость или расплывчатость. Ошибки принятия решений по управлению проектами, в основном, складывается из ошибок и неточностей исходных данных, ошибок и неточностей модели, неточностей и ошибок метода решения, нечеткости человеческого мышления[4].

Автор статьи предлагает осуществлять моделирование процесса принятия решений по управлению проектами в условиях неопределенности на основе теории нечетких множеств. Существуют преимущества описания процесса принятия решений в сложной многоуровневой иерархической системе управления проектами на основе теории нечетких множеств. Эти преимущества состоят в возможности адекватно моделировать сущность процесса принятия решений, оперировать с нечеткими ограничениями и целями, а также задавать их с помощью лингвистических переменных.

Для реальных сложных систем управления проектами характерно наличие одновременно разнородных видов информации и неопределенностей:

- значений различных нормативов параметров работ - детерменированная информация;

- допустимых интервалов изменения величин - интервальная неопределенность;

- статистических законов распределения для отдельных параметров и характеристик проекта - стохастическая неопределенность;

- качественных, лингвистических критериев и ограничений - лингвистическая неопределенность.

Поэтому при управлении проектами приходится ориентироваться на самое неблагоприятное сочетание видов неопределенности. Существование в сложной многоуровневой системе управления проектами одновременно различных видов неопределенности делает необходимым использование для принятия решений теории нечетких множеств, которая позволяет адекватно учитывать различные виды неопределенности.

В реальном управлении проектами при нечетко-множественном подходе резкой грани между альтернативными вариантами решения ЗПР УПнет, так как незначительное изменение значения параметра работ проекта х ведет лишь к небольшому изменению значения функции принадлежности 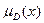. Ограничения на допустимость решения задач управления проектами также могут быть четкими и нечеткими. Применение нечетких ограничений значительно расширяет возможности управления и делает их адекватными для сложной системы управлении проектами. Нет необходимости в получении оптимального четкого решения для каждого момента времени, ведь затраты на накопление информации и жесткое устранение неточностей в системе могут превышать достигаемый при этом эффект.

Учет фактора неопределенности при решении задач управления проектами изменяют методы принятия решения: меняется принцип представления исходных данных и параметров модели, становятся неоднозначными понятия решения задачи и оптимальности решения. При рассмотрении процесса принятия решений по УП в нечётких условиях существует симметрия, равнозначность по отношению к целям и ограничениям. Эта равнозначность стирает различия между целями и ограничениями и позволяет довольно просто сформировать на их основе решение.

Рассмотрим обобщенную формализованную модель задачи принятия решений по управлению проектами, которая имеет следующий вид[3]:

M= (X, Y, S, D, F),

где X -множество альтернативных решений ЗПР УП;

Y -векторный критерий оценки решений ЗПР УП;

S -система упорядоченных оценок;

D -множество допустимых векторных оценок ЗПРУП;

F - отображение множества альтернативных решений в множество допустимых векторных оценок;

G - множество ограничений ЗПР УП.

Пусть заданы нечеткие цели Y= { Y_i } в множестве альтернатив X ЗПР УП; y_i= {(x, 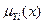) / xÎX; 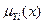- функции принадлежности к нечетким целям Y_i,; i= 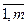}и ограничения G = { G_j }; G_j = {(х, 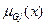)/ xÎ X; 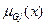-функции принадлежности к нечетким ограничениям G_j; j = 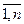}. Нечёткая цель ЗПР УП отождествляется с фиксированным нечётким подмножеством множества X и нечёткое ограничение в пространстве X определяется как некоторое нечеткое подмножество в множестве альтернатив X, т.е. и цель и ограничения ЗПР УП рассматриваются как нечёткие множества в пространстве альтернатив - не делается принципиального различия между целями и ограничениями при формировании решения.

Решение ЗПР УП - это выбор одной или нескольких из имеющихся альтернатив множества X и формально определяется как нечеткое множество D:

D=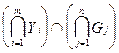

с функцией принадлежности:

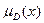=min(,…, , ,…, ).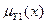

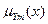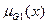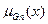В нечёткое решение цели и ограничения входят в выражение для D совершенно одинаковым образом, что и соответствует равнозначности целей и ограничений в процессе принятия решений в нечётких условиях.

При решении ЗПР УП выбирают те альтернативы, которые имеют максимальную степень принадлежности к D. Если таких элементов несколько, то они образуют множество, которое называется оптимальным решением, а каждый элемент этого множества – максимизирующим решением.

Часто встречаются ситуации, в которых некоторые цели или некоторые ограничения ЗПРУП являются более важными и приоритетными, чем остальные. В таких случаях можно ввести весовые коэффициенты a_i и b_j относительной важности целей Y ₁, Y ₂,…, Y _m и ограничений G ₁, G ₂,…, G _n и решение D может быть представлено в следующем виде:

D= ,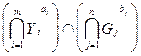

где a_i и b_j - весовые коэффициенты, такие, что

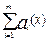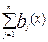+ =1.

В частности, если m=n =1, получится любое нечеткое множество, содержащееся в Y 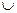G и включающее Y 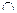G.

Рассмотрим нечеткий процесс по УП, который можно представить следующим образом.

Пусть РR ={ pr ₁, рr ₂,..., рr _i,..., рr _l} — множество признаков, характеризующих нечеткий процесс управления проектами. Признаки р_i, i = {1, 2,..., l }, где l- число признаков, описываются соответствующими лингвистическими переменными

< pr_i, T_i, D_i >,

где T_i ={ T ₁ ⁱ , T ₂ ⁱ , T ₃ ⁱ ,…, T _Mi ⁱ }-терм-множество лингвистической переменной;

М_i -число значений признака pr_i;

D_i -базовое множество признака pr_i.

Получение нечеткого значения параметра или признака может быть получено следующим образом. Обычно имеется возможность наряду с наиболее допустимым значением параметра проекта указать минимальное и максимальное значение (интервал), которые может принимать нечеткая величина данного параметра признака. Иногда удается построить для него характеристическую функцию, показывающую допустимость каждого значения внутри интервала, что дает возможность проводить вычисления не с одним точечным значением, а с характеристической функцией и получать в результате вычислений нечеткую величину, для которой по максимуму значения функции может быть получена точечная (четкая) оценка.[5]

Рассмотрим пример задачи принятия решений по управлению проектами: выбор варианта наиболее осуществимого проекта на стадии инициации. Если имеется несколько допустимых к реализации проектов, то необходимо провести предварительный анализ проектов и выбрать из множества различных проектов наиболее осуществимый по комплексу обобщенных характеристик проекта в целом.

Автор статьи предлагает повысить обоснованность принимаемого решения по выбору наиболее осуществимого проекта из множества допустимых на основе метода пересечения нечетких множеств. Суть данного метода состоит в том, чтобы при имеющихся альтернативах (возможных проектах) и критериях, оценки по которым представлены нечеткими множествами, найти оптимальную альтернативу (проект) по результатам пересечения нечетких множеств[2].

На стадии инициации и предварительного анализа проекта мы предлагаем оценивать проекты по следующему множеству критериев оценки проектов С= { C ₁,…, C ₁₀},где С ₁-конкурентоспособность продукции проекта, С ₂-сложность проекта, С₃ -наличие альтернативных технических решений, С₄ -спрос на продукцию проекта, С ₅-продолжительность проекта, в том числе его инвестиционной фазы, С ₆-уровень базовых, текущих и прогнозных цен на продукцию (услуги) проекта, С ₇-перспективы экспорта продукции проекта, С ₈-исходно-разрешительная документация, С ₉-инвестиционный климат в регионе реализации проекта, С ₁₀-соотношение затрат и результатов проекта. Оценки проекта по данным критериям представляются нечеткими множествами и определяются экспертами[4]. В этом случае имеем множество критериев оценки и единственную нечеткую цель -наиболее осуществимый проект.

Нами предлагается выбирать проект, наиболее осуществимый в нечетких условиях, с помощью следующего макроалгоритма.

Шаг 1. Задать множество возможных проектов 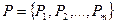и множество критериев оценки их осуществимости .

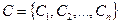Шаг 2. Определить с помощью экспертов оценки проектов по каждому i -му критерию нечеткими множе­ствами:

, ,

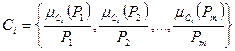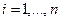где 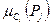- значение функции принадлежности нечеткой оценки проекта P_j по критерию C_i

Шаг 3. Определить весовые коэффициенты критериев на основании матрицы попарных сравнений критериев.

Шаг 4. Найти пересечение нечетких множеств, соответствующих каждому критерию С _i, :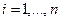

,

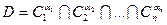где 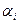- весовой коэффициент, соответствующий критерию i. Весовые коэффициенты должны удовлетворять следующим условиям:

; ; .

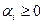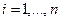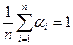При этом функция принадлежности результата пересечения определяется следующим образом:

, .

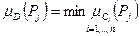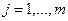Шаг 5. Выбрать наиболее осуществимый проект P*, который соответствует максимальному значению функции принадлежности результата пересечения нечетких множеств:

, .

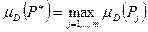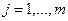Данный алгоритм позволяет не только выбирать наиболее осуществимый проект, но и ранжировать проекты по степени их осуществимости, в порядке убывания значения функции принадлежности. Кроме того, алгоритм может быть легко перенастроен на определение проекта с другими характеристиками, например, на выбор проекта, обладающего наименьшей степенью риска.

Таким образом, автором предложен подход к моделированию процесса принятия решений по управлению проектами в условиях неопределенности на основе теории нечетких множеств и обосновано преимущество такого подхода. Для оценки осуществимости проекта определены критерии оценки проектов и разработан алгоритм выбора наиболее осуществимого проекта, базирующийся на методе пересечения нечетких множеств, который позволяют ЛПР повысить обоснованность принимаемого решения по выбору наиболее осуществимого проекта из множества допустимых.

Список литературы

1. Алтунин, А.Е. Модели и алгоритмы принятия решений в не­четких условиях / А.Е. Алтунин, М.В. Семухин.– Тюмень: Изд-во Тюменьского государственного университета, 2000. – 352 с.

2. Андрейчиков, А.В. Анализ, синтез и планирование ре­шений в экономике/ А.В. Андрейчиков, О.Н. Андрейчикова.– М.: Финансы и статистика, 2000.–363с.

3. Арсеньев, Ю.Н. Информационные системы и технологии. Экономика. Управление. Бизнес: Учебное пособие/Ю.Н. Арсеньев, С.И. Шелобаев, Т. Ю. Давыдова.-М.: ЮНИТИ_ДАНА, 2006,-447 с.

4. Мазур, И.И. Управление проектами / И.И Мазур., В.Д Шапиро., Н.Г. Ольдерогге.- М.: Омега-Л, 2004.-664 с.

5. Ротштейн, А.П. Интеллектуальные технологии идентификации: нечеткая логика, генетические алгоритмы, нейронные сети/ А.П.Ротштейн. — Винница: УНИВЕРСУМ—Винница, 1999. — 320 с.

УПРОЩЕННЫЙ ВАРИАНТ МЕТОДА АНАЛИЗА ИЕРАРХИЙ НА ОСНОВЕ АДДИТИВНОЙ СВЕРТКИ КРИТЕРИЕВ ДЛЯ РЕШЕНИЯ ЗАДАЧИ оптимального распределения премиального фонда

М.А. Беляева, Е.А. Букина

В настоящее время методы теории принятия решений применяется в самых различных областях [1] - при проектировании сложных технических и организационных систем, выборе программ развития экономики и энергетики регионов, организации новых экономических зон и др.

В упрощенном варианте метода анализа иерархий [4] процедуру формирования матрицы парных сравнений предлагается существенно упростить, требуя от эксперта сведения не обо всех элементах этой матрицы, расположенных выше (ниже) главной диагонали, а лишь об определенных «базисных» элементах, на основе которых затем легко находится весовой вектор. При этом выбор конкретного «базисного» набора соответствует той или иной схеме сравнения объектов, которую можно выбирать с целью получения наиболее надежных результатов от эксперта. В упрощенном варианте метода анализа иерархий определяется матрица парных сравнений только на основе введенных экспертом элементов первой строки такой матрицы, что существенно упрощает формирование матрицы парных сравнений. Кроме того, сформированная таким образом матрица парных сравнений всегда обладает важным свойством совместности, которое на практике формирования матрицы парных сравнений часто нарушается.

Рассмотрим применение упрощенного варианта метода анализа иерархий для решения задач оптимального распределения с учетом многих критериев на примере задачи оптимального распределения премиального фонда между работниками предприятия.

Распределение премиального фонда между работниками предприятия в соответствии с коэффициентами трудового участия на практике осуществляется достаточно часто. Основная трудность такого распределения - определение коэффициента трудового участия каждого из премируемых на основании множества различных показателей, в соответствии с которыми учитывается трудовой вклад каждого работника. Авторы статьи предлагают определять коэффициенты трудового участия работников на основе синтеза методов теории принятия решений - упрощенного варианта метода анализа иерархий и метода аддитивной свертки критериев.

Пусть требуется распределить премиальный фонд между m работниками (альтернативами) и определить коэффициенты трудового участия каждого работника по n трудовым показателям (критериям) [2].

Нами разработан алгоритм решения задачи оптимального распределения премиального фонда на основе синтеза упрощенного варианта метода анализа иерархий и аддитивной свертки критериев [3].

Шаг 1. Ввод матрицы B=[b_ij], i=1,…,m, j=1,…n оценок альтернатив по критериям и размера премиального фонда C.

Шаг 2. Ввод экспертом первой строки матрицы парных сравнений критериев A=[a_ij], i=1,…,n, j=1,…n, в которой сравнивается первый критерий со всеми остальными.

Шаг 3. Расчет матрицы парных сравнений A=[a_ij] на основе первой строки по формуле:

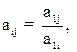
(1)

где 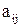- элемент матрицы парных сравнений, i=1,…,n, j=1,…n;

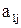- элемент j первой строки матрицы парных сравнений, j=1,…n;

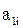- элемент i первой строки матрицы парных сравнений, i=1,…,n.

Шаг 4. Расчет вектора приоритетов критериев w = (w₁, w₂,..., w_n)^Т производится по формуле:

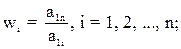
(2)

где 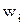- компонента i вектора приоритетов, i=1,…,n;

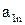- элемент последнего столбца матрицы парных сравнений;

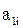- элемент i первой строки матрицы парных сравнений, i=1,…,n.

Шаг 5. Нормировка вектора приоритетов критериев W = (w₁,w₂,..., w_n)^Т производится по формуле:

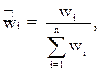(3)

где 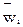- нормированный компонент i вектора приоритетов, i=1,…,n;

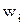- компонент i вектора приоритетов, i=1,…,n.

Шаг 6. Нормирование матрицы B=[b_ij]. i=1,…,m, j=1,…n. оценок альтернатив по критериям.

Шаг 7. По методу аддитивной свертки вычисляется вектор приоритетов альтернатив F=(f₁, f₂,..., f_m):

f_i= 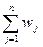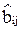, (4)

где f_i- элемент i вектора приоритетов альтернатив, i=1,…,m;

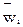- нормированный компонент i вектора приоритетов;

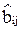- нормированный элемент матрицы B, j=1,…n.

Шаг 8. Расчет премиального фонда в соответствии с найденным приоритетом альтернатив:

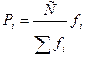, (5)

где 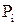- размер премии альтернативы i, i=1,…,m;

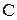- размер премиального фонда;

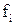- элемент i вектора приоритетов альтернатив, i=1,…,m.

Данный алгоритм реализован на ЭВМ при распределении премиального фонда между бригадами по ремонту скважин ООО «Промтех» г. Сорочинска и показал свою эффективность. Распределение премиального фонда производились на основе следующих трудовых показателей:

- объемы выполненных блоков работ;

- качество выполненных работ;

- простои по вине бригады;

- приоритеты работ.

Качество работ и простои бригад являются экспертными оценками[2] и задавались экспертами.

Матрица парных сравнений, рассчитанная по формуле (1) имеет следующий вид:

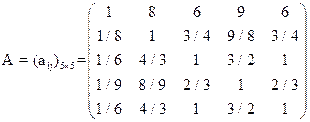
Вектор приоритетов критериев, рассчитанный по формуле (2) имеет следующий вид:

w = (6, 3/4, 1, 2/3, 1)^Т.

После нормировки по формуле (3) вектор приоритетов критериев примет следующий вид:

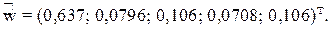
Нормированная матрица оценок альтернатив по критериям имеет следующий вид:

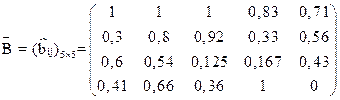
Вектор приоритетов альтернатив, найденный по формуле (4) имеет следующий вид:

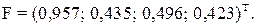
В соответствии с формулой (5) вектор премии имеет следующий вид:

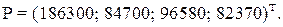
Результаты расчетов представлен на рисунке 1.

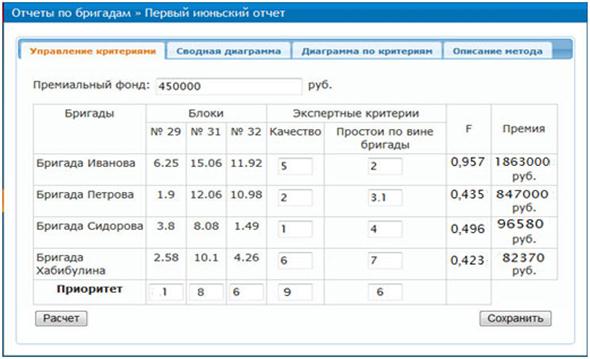
Рисунок 1 - Экранная форма результатов вычислений

Для наглядности результаты представлены графически в виде диаграмм, которые изображены на рисунке 2.

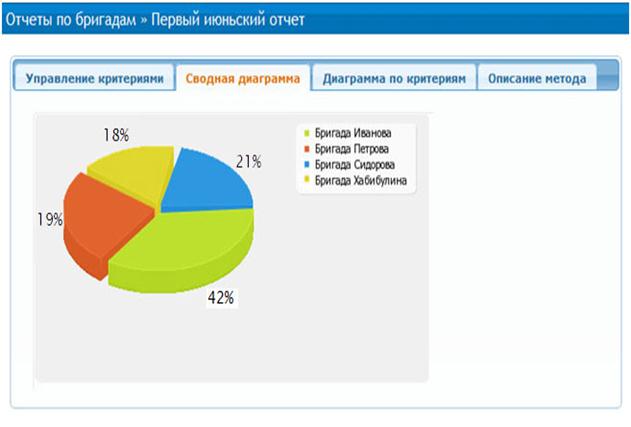
Рисунок 2 - Экранная форма сводной диаграммы

Упрощенный вариант метода анализа иерархий на основе аддитивной свертки значительно сокращает время при формировании матрицы парных сравнений, уменьшает ошибки вычислительного характера и позволяет эффективно решать задачи многокритериальной оптимизации. Матрица парных сравнений, сформированная по данному методу всегда обладает важным свойством совместности. Разработанный нами алгоритм позволяет осуществлять распределение премиального фонда между работниками (альтернативами) в соответствии с коэффициентами трудового участия каждого работника.[2].

Список литературы

1. Андрейчиков, А.В. Анализ, синтез и планирование ре­шений в экономике/ А.В. Андрейчиков, О.Н. Андрейчикова.– М.: Финансы и статистика, 2000.–363с.

2. Арсеньев, Ю.Н. Принятие решений. Интеллектуальные интегрированные системы: Учебное пособие для вузов/Ю.Н. Арсеньев, С.И. Шелобаев, Т. Ю. Давыдова.-М.: ЮНИТИ_ДАНА, 2006,-447 с.

3. Бережная, Е.В., Математические методы моделирования экономических систем: Учебное пособие/ Е.В Бережная, В.И Бережной. - М.: Финансы и статистика, 2001.-368 с.

4. Ногин, В.Д. Упрощенный вариант метода анализа иерархий на основе нелинейной свертки критериев/ В.Д. Ногин.- СПб.: БХВ-Петербург, 2004.