Кортеж. Прямое произведение множеств

Определение 44. Множество 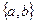называется неупорядоченной парой или просто парой, если выполняется свойство: .

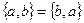Определение 45. Множество 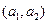называется упорядоченной парой, если указано, какой из этих элементов первый, какой второй, при этом 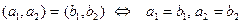, в частности = .

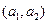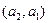
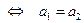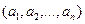– упорядоченная система из n элементов. (n -ка элементов). Элементы а ₁, а ₂, …, а_n называются координатами упорядоченной системы.

Определение 46. Кортеж – последовательность элементов, т.е. совокупность элементов, в которой каждый элемент занимает определенное место.

Например, множество людей в очереди.

Определение 47. Число элементов в кортеже называется его длиной.

Кортеж длины нуль называется пустым.

Иначе определение 46. Кортеж или упорядоченная n -ка элементов – упорядоченный набор длины n (где n – любое натуральное число либо нуль): 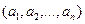, каждый элемент которого принадлежит некоторому множеству.

Элементы кортежа называются его компонентами, или координатами и могут повторяться в нём любое число раз (этим, в частности, он отличается от упорядоченного множества, куда каждый элемент может входить только в одном экземпляре).

Упорядоченная пара – частный случай кортежа.

Примеры кортежей: 1) пустое множество – кортеж (с нулевым количеством элементов), 2) для каждого кортежа 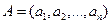множество 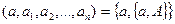также является кортежем, 3) точка в n -мерном пространстве действительных чисел определяется как кортеж длины n, составленный из элементов множества действительных чисел.

Определение 47. Прямым или декартовым произведением двух множеств А и В называется множество 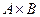всех упорядоченных пар 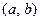, в которых первый элемент 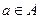, а второй : .

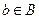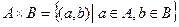Например, если 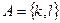, , 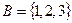то .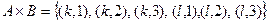

Замечание 1. Обозначение упорядоченной пары может быть таким: < a, b>, прямого произведения –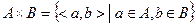

Замечание 2. Элементами прямого произведения являются двухэлементные кортежи вида .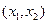

Замечание 3. 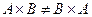, т.е. результат прямого произведения зависит от порядка сомножителей.

Геометрическое представление. Например, если 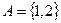, , 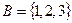тогда 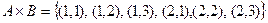, и геометрически прямое произведение представляется в виде точек: