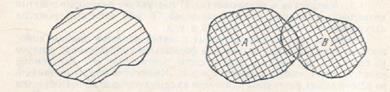
Объединением двух множеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств: 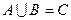 .
.
А È В = {х: хÎА или хÎВ}
Пример
Множество студентов, пришедших на сдачу экзамена, является объединением множеств студентов, сдавших экзамен и студентов, получивших неудовлетворительную отметку. Объединением числовых множеств 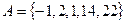 и
и 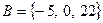 является множество
является множество 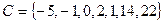 .
.
 |
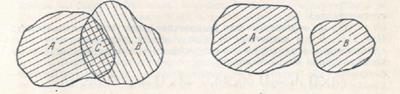
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, принадлежащих одновременно каждому из этих множеств: 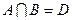 .
.
А Ç В = {х: хÎА и хÎB}.
 |
Пример
Пересечение множества страниц данного учебного пособия и множества страниц, прочитанных Вами в течение сегодняшнего дня в различных печатных работах, есть множество, состоящее из страниц этой тетради, прочитанных Вами сегодня. Пересечение множеств натуральных чисел и чисел, кратных 3, есть множество натуральных чисел, кратных трем.
Cвойства операций объединения и пересечения:
1) коммутативность:
A U В= В U А, А 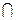 В = В
В = В 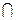 А;
А;
2) ассоциативность:
(А U В) U С = A U (В U С), (А 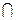 В)
В) 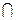 С = А
С = А 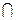 (В
(В 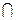 С);
С);
3) дистрибутивность:
(А U В) 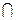 С = (А
С = (А 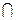 С) U (В
С) U (В 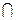 С),
С),
(А 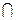 В) U С = (.А U С)
В) U С = (.А U С) 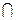 (В U С)
(В U С)
Разностью двух множеств А и В называется множество Е, состоящее из всех элементов множества А, не принадлежащих множеству В: 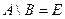 . При этом, не предполагается, что В
. При этом, не предполагается, что В 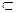 А. Разность множеств А и В обозначается А \ В (или А — В).
А. Разность множеств А и В обозначается А \ В (или А — В).
А \ В= {х: хÎА и хÏВ}.
Пример
Если в качестве множества А рассмотреть двузначные числа, а в качестве множества В четные двузначные числа, то разностью этих множеств будут являться нечетные двузначные числа.
Если В — подмножество А, то разность А \ В также называют дополнением множества В до множества А. Если R = А \ В, то R 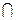 В = Æ и R U В = А.
В = Æ и R U В = А.
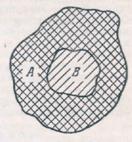
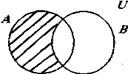
Дополнением множества 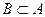 называется множество Вс, состоящее из всех элементов множества А, не принадлежащих В.
называется множество Вс, состоящее из всех элементов множества А, не принадлежащих В.
Пример
Пусть А — множество всех натуральных чисел, кратных двум, а В — множество всех натуральных чисел, кратных трем. Объединением этих множеств будет множество всех натуральных чисел, кратных числу 2 или числу 3. Их пересечением будет множество всех натуральных чисел, кратных как числу 2, так и числу 3, т. е. кратных числу 6.
Пусть теперь А — множество всех натуральных чисел, кратных числу 2, а В — множество всех натуральных чисел, кратных числу 6 (т. е. кратных как числу 2, так и числу 3). Множество В является подмножеством множества А. Дополнением множества В до множества А будет множество всех натуральных чисел, кратных числу 2, но не кратных числу 3.
Понятия объединения и пересечения, данные для случая двух множеств, могут быть распространены и на случай любого числа множеств.
Объединением конечного числа множеств Ai (i= 1, 2,..., n) называют множество В, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств Ai, и пишут
B = 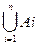
Пересечением конечного числа множеств Ai (i= 1, 2,..., n) называют множество С, состоящее из всех элементов, принадлежащих одновременно всем множествам Ai, и пишут
С = 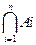 .
.
Если Аi — бесконечная совокупность множеств (i=l, 2,..., n,...), то объединение и пересечение этих множеств обозначают с помощью символов
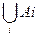 и
и 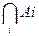
соответственно.
Пусть Аi — конечная или бесконечная совокупность подмножеств (i = 1, 2, 3,...) множества А. Связь между подмножествами Аi и множеством А устанавливается следующими равенствами, называемыми соотношениями двойственности:
A\ 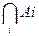 =
=  , А\
, А\ 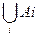 =
= 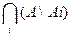 .
.
Пусть А и В — два произвольных множества. Пара (а, b) элементов а 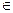 В и b
В и b 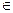 В, взятых в данном порядке, называют упорядоченной парой. Считают, что пары (а1, b1) и (а2, b2) равны тогда и только тогда, когда a1 = a2 и b1 = b2.
В, взятых в данном порядке, называют упорядоченной парой. Считают, что пары (а1, b1) и (а2, b2) равны тогда и только тогда, когда a1 = a2 и b1 = b2.
Декартовым произведением двух множеств А и В называется множество всех упорядоченных пар (а, b). Декартово произведение множеств А и В обычно обозначается А 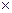 В.
В.
Множества, элементами которых являются действительные числа, называются числовыми. Они представляют для нас наибольший интерес и имеют геометрическую интерпретацию, знакомую Вам еще по школьному курсу.
Множество Х, элементы которого удовлетворяют: - неравенству 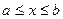 , называется отрезком (или сегментом) , называется отрезком (или сегментом) 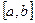 ; - неравенству ; - неравенству 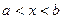 , называется интервалом , называется интервалом 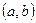 ; - неравенствам ; - неравенствам 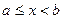 или или 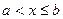 , называется полуинтервалами соответственно , называется полуинтервалами соответственно 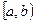 и и 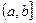 . Наряду с этим рассматриваются бесконечные интервалы и полуинтервалы . Наряду с этим рассматриваются бесконечные интервалы и полуинтервалы 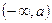 , , 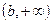 , , 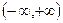 , , 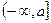 , , 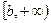 . Все эти множества объединяются термином «промежуток Х». . Все эти множества объединяются термином «промежуток Х». | Обратите внимание на запись множества в виде числового промежутка и в виде неравенства. Попробуйте изобразить указанные множества на числовой прямой. |
Задание 1.1.3. Выполните следующие задания, если 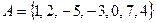 , , 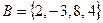 , , 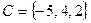 , , 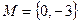 , , 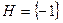 : 1) Выясните, какие из предложенных множеств являются подмножествами множества А и определите для них соответствующие дополнения, 2) Найдите пересечение множеств А и В, В и С, В и Н, 3) Найдите объединение множеств Н и В, В и М, 4) Найдите разность множеств А и В. (Подсказка. Воспользуйтесь приведенными выше определениями и образцами символической записи. Ответ. 1) : 1) Выясните, какие из предложенных множеств являются подмножествами множества А и определите для них соответствующие дополнения, 2) Найдите пересечение множеств А и В, В и С, В и Н, 3) Найдите объединение множеств Н и В, В и М, 4) Найдите разность множеств А и В. (Подсказка. Воспользуйтесь приведенными выше определениями и образцами символической записи. Ответ. 1) 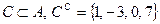 , , 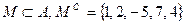 ; 2) ; 2) 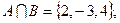 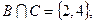 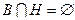 ; 3) ; 3) 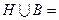 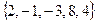 , , 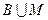 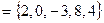 ; 4) ; 4) 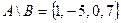 .) .) |
Операции объединения, пересечения, дополнения {È, Ç, } часто называют булевыми операциями над множествами.
Пример
Пусть универсальное множество U- множество всех сотрудников некоторой фирмы; А - множество всех сотрудников данной организации старше 35 лет; В - множество сотрудников, имеющих стаж работы более 10 лет; С -множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств:
а) В;
б) А Ç B Ç С;
в) A È (B Ç С)
г) B \ С;
д) С \ B?
Ø а) В - множество сотрудников организации, стаж работы которых не превышает 10 лет;
б) А Ç В Ç С - множество менеджеров фирмы не старше 35 лет, имеющих стаж работы более 10 лет;
в) А È (В Ç С) - множество всех сотрудников фирмы старше 35 лет, а также сотрудников, не являющихся менеджерами, стаж работы которых более 10 лет;
г) В \ С - множество сотрудников организации со стажем работы более 10 лет, не работающих менеджерами;
д) С \ В - множество менеджеров со стажем работы не более 10 лет.
Пример
Задайте множества М, N, если: М - множество всех натуральных чисел, не превосходящих 100; N - множество натуральных чисел.
Ø М -множество всех натуральных чисел, больших 100. Запись N без контекста (т.е. без указания универсального множества U) не ясна:
• то ли это множество всех отрицательных целых чисел;
• то ли это множество положительных дробных чисел;
• то ли это пустое множество натуральных чисел.
Пример
Осуществите операции над множествами A = {a,b,c,d} и B = {c,d,e,f,g,h}.
Ø A È В= {а, b, с, d, e, f, g, h}; A Ç B={c, d}.
Универсальное множество U не определено, поэтому, строго говоря, операции дополнения над множествами A и В не могут быть выполнены. Дополним условие. Пусть U={a, b, с, d, e, f, g, h}, тогда А = U \ A = {e, f, g, h}, В ={а,b}. A \ B={a,b}; B \ A = {e,f,g,h}.
 2015-05-22
2015-05-22 3812
3812
