Одинаково распределенные взаимно независимые СВ.
Рассмотрим  взаимно независимых СВ
взаимно независимых СВ 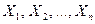 , которые имеют одинаковые распределения, а следовательно и одинаковые характеристики.
, которые имеют одинаковые распределения, а следовательно и одинаковые характеристики.
Обозначим через 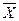 - среднее арифметическое этих величин:
- среднее арифметическое этих величин:
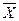 =
= 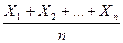 .
.
Связь между числовыми характеристиками среднего арифметического 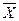 и соответствующими характеристиками каждой отдельной величины устанавливают следующие положения:
и соответствующими характеристиками каждой отдельной величины устанавливают следующие положения:
1. МО среднего арифметического одинаково распределенных взаимно независимых СВ равно математическому ожиданию 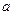 каждой из величин:
каждой из величин:
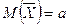 . (1)
. (1)
2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии 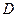 каждой из величин:
каждой из величин:
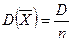 . (2)
. (2)
3. Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в 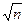 раз меньше среднего квадратического отклонения
раз меньше среднего квадратического отклонения 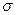 каждой из величин:
каждой из величин:
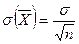 . (3)
. (3)
Пример 1. Дисперсия каждой из 9 одинаково распределенных взаимно независимых СВ равна 36. Найти дисперсию среднего арифметического этих величин. ► по ф-ле (2) 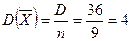 .◄
.◄
 2015-06-10
2015-06-10 1458
1458








