| Наименованиехарактеристики | Генеральная совокупность | Выборка |
| Средняя | 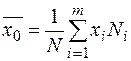 | 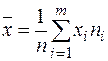 |
| Дисперсия | 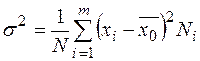 | 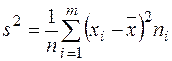 |
| Доля | 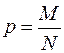 | 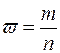 |
Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.
Таблица 2. Оценка параметров генеральной совокупности
по собственно-случайной выборке.
| Параметр | Выборка | Несмещенная и состоятельная оценка | Дисперсия оценки |
| Генеральная доля | Повторная | 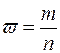 | 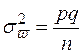 |
| Бесповторная | 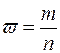 | 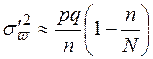 | |
| Генеральная средняя | Повторная | 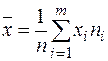 | 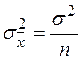 |
| Бесповторная | 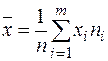 | 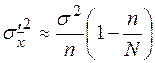 | |
| Генеральная дисперсия | Повторная и бесповторная | 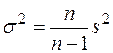 |
Среднее квадратическое отклонение выборочной средней 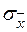 и выборочной доли
и выборочной доли 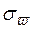 собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки. (Для бесповторной выборки обозначения – соответственно
собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки. (Для бесповторной выборки обозначения – соответственно 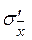 и
и 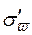 ).
).
Формулы доверительной вероятности для средней 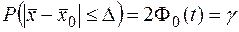
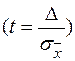 и доли
и доли 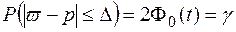
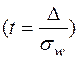 .
.
При заданной доверительной вероятности g предельная ошибка выборки равна t-кратной величине средней квадратической ошибки, где 2F0(t) = g, т.е. 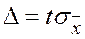 ,
, 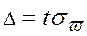 .
.
Интервальные оценки (доверительные интервалы) для генеральной средней и генеральной доли могут быть найдены по формулам:  ,
, 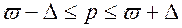 .
.
Таблица 3. Формулы средних квадратических ошибок выборки
| Оцениваемый параметр | Повторная выборка | Бесповторная выборка |
| Генеральная средняя | 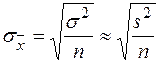 | 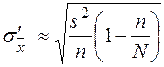 |
| Генеральная доля | 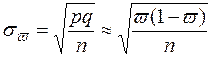 | 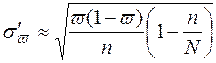 |
Таблица 4. Определение объема выборки по доверительной вероятности g и предельной ошибке выборки D
| Оцениваемый параметр | Повторная выборка | Бесповторная выборка |
| Генеральная средняя | 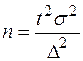 | 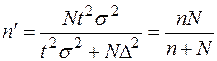 |
| Генеральная доля | 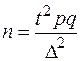 | 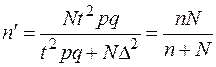 |
19.1. Отдел технического контроля электролампового завода хочет узнать срок службы (время горения) отдельного вида лампочек. С этой целью случайная выборка 80 лампочек была испытана на продолжительность горения. Выборочная средняя равняется 2915 ч, а выборочное среднее квадратическое отклонение 396 ч. Найти вероятность того, что средний срок службы лампочек данного вида отличается от выборочной средней не более, чем на 90 ч (по абсолютной величине).
19.2. Случайная выборка 800 школьников показала, что 480 из них хотела бы заниматься в школе в первую смену. Определить границы, в которых с вероятностью 0,9 заключена доля всех школьников, которые хотели бы учиться в первую смену.
19.3. Отдел сбыта кондитерской фабрики при опросе 200 жителей города А, отобранных по схеме собственно-случайной бесповторной выборки, обнаружил, что для 50 из них желательно изменение ассортимента продукции. Отдел наметил провести такое же обследование в городе Б. Найти: а) 95 %-й доверительный интервал для доли потребителей в городе А, которые будут покупать новые виды продукции; б) объем выборки в городе Б, чтобы достичь оценки доли потребителей новой продукции в пределах ± 4 % с доверительной вероятностью 0,95.
19.4. По схеме собственно-случайной бесповторной выборки было отобрано 100 студентов из 500 обучающихся и получены следующие данные о времени решения задачи по теории вероятностей:
| Время решения задачи, мин | |||||
| Количество студентов |
Найти: а) вероятность того, что среднее время решения задачи в выборке отличается от среднего времени решения задачи во всей генеральной совокупности не более чем на 1 мин (по абсолютной величине); б) число студентов, которое нужно отобрать в выборку, чтобы то же отклонение гарантировать с вероятностью 0,9876; в) границы, в которых с вероятностью 0,9596 заключена доля студентов, решавших задачу не более 9 мин.
19.5. Для определения рейтинга мэра города было опрошено 200 человек. Выборочный рейтинг оказался равным 0,4. Определить необходимое количество респондентов, гарантирующее с вероятностью 0,9802 ошибку социологического обследования, не превосходящую 2 %.
19.6. Проводится сравнительный анализ старого и нового метода сборки некоторого изделия. Среднее время сборки по старому методу составляет 90 мин. Для оценки нового метода сборки по схеме бесповторной собственно-случайной выборки были отобраны 100 рабочих из 500. Получено следующее распределение рабочих по продолжительности сборки:
| Продолжительность сборки, мин | |||||
| Число рабочих |
Найти: а) доверительный интервал с вероятностью 0,95 для среднего времени сборки по новому методу; б) наименьший размер выборки, необходимый для получения среднего значения генеральной совокупности в пределах двух минут с доверительной вероятностью 0,9901.
19.7. Маркетинговое исследование показало, что реализуемый фирмой товар требуется 16 из 200 опрашиваемых. Фирма разворачивает свою деятельность в районе с населением 20000 человек. Найти границы, в которых с вероятностью 0,95 будет заключено количество покупателей.
19.8. Торговая фирма получила от поставщика пробную партию из 100 стиральных машин. Среди них оказалось 5 с дефектами. Найти вероятность того, что доля стиральных машин с дефектами во всей партии из 5000 штук отличается от таковой в выборке не более чем на 0,02.
19.9. Из 620 студентов-первокурсников БГТУ было отобрано по схеме собственно-случайной бесповторной выборки 100 студентов, из которых оказалось 60 проживающих в г. Брянске. Найти границы, в которых с вероятностью 0,9545 заключен процент студентов – жителей г. Брянска среди всех студентов первого курса.
19.10. По схеме собственно-случайной бесповторной выборки из общего большого числа стальных проволок, идущих на изготовление канатов, были отобраны 150 и проведены испытания на растягивающее усилие. Оказалось, что проволока выдерживает в среднем усилие в 67,2 кН/см2 , а выборочное среднее квадратическое отклонение равно 2,2 кН/см2. Найти: а) границы, в которых с вероятностью 0,9975 заключено среднее разрывное усилие проволок всей партии; б) вероятность того, что среднее разрывное усилие всех проволок в партии не отличается от среднего разрывного усилия в выборке не более чем на 0,3 кН/см2; в) объем выборки, для которой доверительные границы с предельной ошибкой D = 0,5 имели бы место с доверительной вероятностью 0,9910.
 2015-06-10
2015-06-10 1610
1610
