Закон распределения двумерной дискретной случайной величины задаётся таблицей
| Y X | 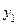 | 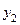 | … | 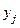 | … | 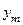 |
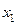 | 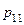 | 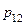 | … | 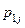 | … | 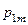 |
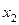 | 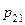 | 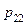 | … | 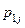 | … | 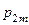 |
| … | … | … | … | … | … | … |
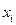 | 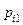 | 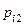 | … | 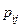 | … | 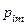 |
| … | … | … | … | … | … | … |
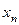 | 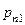 | 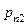 | … | 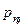 | … | 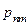 |
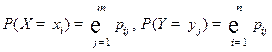 .
.
Корреляционным моментом (ковариацией) системы двух случайных величин называется число, равное Kxy = M ((X – M (X))(Y – M (Y))). Для дискретных случайных величин 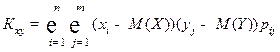
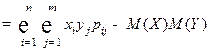 .
.
Линейная средняя квадратическая регрессия Y на Х имеет вид: 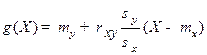 .
.
149. Задан закон распределения двумерной случайной величины (Х,Y)
| Y Х | |||
| 0,10 | 0,20 | 0,15 | |
| 0,05 | 0,14 | 0,11 | |
| 0,12 | 0,08 | 0,05 |
Составить законы распределения составляющих, условный закон распределения случайной величины Х при условии, что Y = 4. Найти коэффициент корреляции между случайными величинами Х и Y. Составить уравнение линейной средней квадратической регрессии Y на Х.
 2015-06-10
2015-06-10 982
982

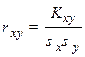 .
.






