1.1. Движение свободных ионов
Понятие “свободный ион” подразумевает, что магнитный момент ядра или атома не испытывает взаимодействия с другими атомами вещества, и, строго говоря, применимо лишь к очень разреженным газам. В твёрдых телах атомы связаны друг с другом силами электростатического и магнитного взаимодействия; однако приближение свободных спинов оказывается здесь полезным для установления характера движения элементарных магнитных моментов под действием постоянного и переменного магнитных полей.
Ядерный момент количества движения G выражают через безразмерный спиновый вектор I и записывают в виде
G = ħ I,
где 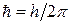 – постоянная Планка. Величиной ядерного спина I называют максимально возможное значение компоненты I в каком-нибудь направлении (например, заданном внешним магнитным полем). Ядерный спин не идентичен с длиной спинового вектора, а связан с ней соотношением
– постоянная Планка. Величиной ядерного спина I называют максимально возможное значение компоненты I в каком-нибудь направлении (например, заданном внешним магнитным полем). Ядерный спин не идентичен с длиной спинового вектора, а связан с ней соотношением 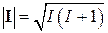 .
.
Ядерный магнитный дипольный момент m параллелен или антипараллелен вектору момента количества движения G, поэтому мы можем написать
m = g G = 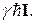
Величина g, называемая гиромагнитным отношением, положительна, если магнитный момент параллелен спиновому, и отрицательна в противном случае. Ядерные магнитные моменты принято измерять в ядерных магнетонах
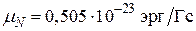
(ср. с магнетоном Бора 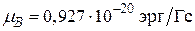 ).
).
На магнитный диполь m, помещенный в магнитное поле H, действует момент силы 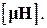 Этот момент силы вызывает изменение во времени вектора момента количества движения G, так что мы можем записать
Этот момент силы вызывает изменение во времени вектора момента количества движения G, так что мы можем записать
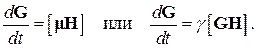 (1)
(1)
Согласно решению этого уравнения, векторы G и m прецессируют вокруг направления поля H с угловой скоростью 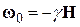 . Каким представится это движение наблюдателю, если он находится в системе координат, которая вращается вокруг оси, совпадающей с направлением вектора Н? Если такая система координат вращается относительно лабораторной системы координат с угловой скоростью w, то производная
. Каким представится это движение наблюдателю, если он находится в системе координат, которая вращается вокруг оси, совпадающей с направлением вектора Н? Если такая система координат вращается относительно лабораторной системы координат с угловой скоростью w, то производная 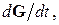 вычисленная в лабораторной системе, и аналогичная производная
вычисленная в лабораторной системе, и аналогичная производная 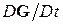 , вычисленная во вращающейся системе, связываются уравнением
, вычисленная во вращающейся системе, связываются уравнением
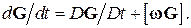
Комбинируя это уравнение с предыдущим, мы получаем уравнение движения
момента G во вращающейся системе координат
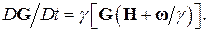 (2)
(2)
Это уравнение похоже на исходное, но отличается от него тем, что вместо Н мы имеем теперь 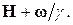 Таким образом, движение векторов G и
Таким образом, движение векторов G и 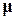 во вращающейся системе координат также представляет собой прецессию, но с угловой скоростью
во вращающейся системе координат также представляет собой прецессию, но с угловой скоростью
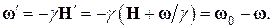 (3)
(3)
Как и следовало ожидать, эта кажущаяся скорость прецессии равна разности между частотой Лармора 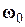 и угловой частотой вращения подвижной системы координат относительно фиксированной. Иначе говоря, во вращающейся системе координат действует эффективное магнитное поле, параллельное оси z и равное
и угловой частотой вращения подвижной системы координат относительно фиксированной. Иначе говоря, во вращающейся системе координат действует эффективное магнитное поле, параллельное оси z и равное
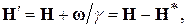 (4)
(4)
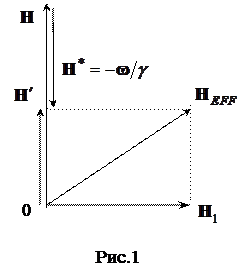 где
где 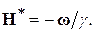 Ясно, что при выполнении равенства
Ясно, что при выполнении равенства 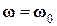 прецессия исчезает, и оба вектора G и m становятся неподвижными во вращающейся системе координат; это соответствует равенству нулю эффективного поля
прецессия исчезает, и оба вектора G и m становятся неподвижными во вращающейся системе координат; это соответствует равенству нулю эффективного поля 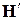 .
.
Используя полученный результат, легко определить движение моментовпри одновременном воздействии постоянного поля H, которое мы предполагаем направленным вдоль оси z декартовой системы координат, и поля 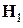 , вращающегося вокруг оси z с угловой скоростью w (см. рис.1). Очевидно, если мы перейдем к координатной системе, также вращающейся вокруг оси z с угловой скоростью w, то поле
, вращающегося вокруг оси z с угловой скоростью w (см. рис.1). Очевидно, если мы перейдем к координатной системе, также вращающейся вокруг оси z с угловой скоростью w, то поле 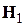 представится в этой системе постоянным вектором, перпендикулярным оси z. В то же время постоянное поле Н должно быть заменено эффективным полем
представится в этой системе постоянным вектором, перпендикулярным оси z. В то же время постоянное поле Н должно быть заменено эффективным полем
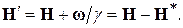 Теперь уравнение движения момента G во вращающейся системе координат принимает вид
Теперь уравнение движения момента G во вращающейся системе координат принимает вид
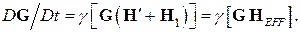 (5)
(5)
Здесь 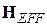 – векторная сумма
– векторная сумма 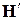 и
и 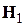 . Это уравнение движения также имеет форму исходного уравнения. Следовательно, во вращающейся системе координат момент количества движения G и магнитный момент m будут испытывать прецессию вокруг вектора
. Это уравнение движения также имеет форму исходного уравнения. Следовательно, во вращающейся системе координат момент количества движения G и магнитный момент m будут испытывать прецессию вокруг вектора 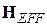 с угловой скоростью
с угловой скоростью 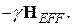
Предположим, что 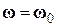 , и что вращающееся поле
, и что вращающееся поле 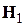 включается мгновенно в момент времени
включается мгновенно в момент времени 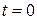 , когда магнитный момент направлен вдоль поля
, когда магнитный момент направлен вдоль поля 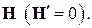 Тогда движение магнитного момента будет представлять собой прецессию вокруг вектора
Тогда движение магнитного момента будет представлять собой прецессию вокруг вектора 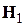 , причем в течение каждого полупериода этого движения направление m будет меняться от параллельного полю Н до антипараллельного и наоборот. Во вращающейся системе координат это движение происходит в плоскости, перпендикулярной
, причем в течение каждого полупериода этого движения направление m будет меняться от параллельного полю Н до антипараллельного и наоборот. Во вращающейся системе координат это движение происходит в плоскости, перпендикулярной 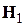 . Поскольку H 1<< H, частота прецессии вокруг
. Поскольку H 1<< H, частота прецессии вокруг 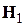 намного меньше
намного меньше 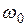 ; так что в лабораторной системе координат движение вектора m представляет собой быстрое вращение вокруг поля Н с одновременным медленным изменением угла a = (m,H) от 0 до p и обратно.
; так что в лабораторной системе координат движение вектора m представляет собой быстрое вращение вокруг поля Н с одновременным медленным изменением угла a = (m,H) от 0 до p и обратно.
Если частота вращения 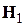 не равна ларморовской частоте прецессии, магнитный момент m во вращающейся системе координат прецессирует вокруг поля
не равна ларморовской частоте прецессии, магнитный момент m во вращающейся системе координат прецессирует вокруг поля 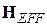 . Это поле составляет с направлением Н угол q, определяемый выражением
. Это поле составляет с направлением Н угол q, определяемый выражением
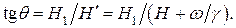 (6)
(6)
Значение угла a в момент времени t (предполагается, что a = 0 при t = 0) находится из простых геометрических соотношений (см. рис.2):
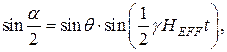 (7)
(7)
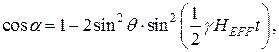
где 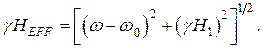
Ясно, что максимальное значение a равно 2 q и, если H 1<< H (нормальный случай), это значение велико только тогда, когда величина w достаточно близка к 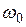 .
.
 Таким образом, эффект носит резонансный характер; в этой возможности заметно изменить ориентацию магнитного момента m относительно постоянного поля Н путём воздействия относительно малым вращающимся полем
Таким образом, эффект носит резонансный характер; в этой возможности заметно изменить ориентацию магнитного момента m относительно постоянного поля Н путём воздействия относительно малым вращающимся полем 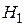 и состоит явление магнитного резонанса. Когда
и состоит явление магнитного резонанса. Когда 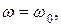 магнитный момент m под действием вращающегося поля
магнитный момент m под действием вращающегося поля 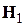 может быть повёрнут на 180°. В идеальном случае это произойдёт при любом значении поля
может быть повёрнут на 180°. В идеальном случае это произойдёт при любом значении поля 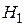 , каким бы малым оно не было, хотя, конечно, скорость переворачивания пропорциональна величине
, каким бы малым оно не было, хотя, конечно, скорость переворачивания пропорциональна величине 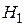 .
.
1.2. Магнитный резонанс в системах связанных спинов
1. Имея дело со связанной системой постоянных магнитных диполей, удобнее оперировать намагниченностью М или магнитным моментом всей системы, нежели магнитными моментами индивидуальных частиц. Магнитный момент всей системы представляет собой просто векторную сумму отдельных магнитных моментов. Поэтому в целом система спинов будет подчиняться классическому уравнению движения
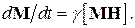 (8)
(8)
Нас интересуют системы, в которых индивидуальные диполи слабо взаимодействуют друг с другом, т.е. такие, для которых статическая магнитная восприимчивость в приближении высоких температур mH/kT << 1 подчиняется закону Кюри:
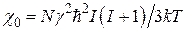 (9)
(9)
(N – число частиц).
2. Особенности магнитного резонанса в системе связанных спинов мы учтём, отказавшись от предположения, что все изменения ориентации и величины намагниченности всецело обусловлены внешними магнитными полями, и приняв во внимание дополнительно два основных типа внутренних взаимодействий в конденсированных средах: 1) взаимодействие диполей с тепловыми колебаниями решётки и 2) взаимодействие их друг с другом. Оба этих взаимодействия обычно намного слабее зеемановского взаимодействия с внешними полями, но имеют значение благодаря их совокупному действию в течение длительных промежутков времени. Основное различие между ними состоит в том, что только первое взаимодействие (тепловые возмущения) может изменить энергию спин-системы, тогда как второе оставляет эту энергию неизменной.
Основную часть энергии спин-системы составляет зеемановская энергия в постоянном магнитном поле 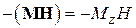 . Следовательно, основные изменения в энергии обязаны изменениям компоненты намагниченности
. Следовательно, основные изменения в энергии обязаны изменениям компоненты намагниченности 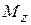 . Предположим, что в какой-то момент времени компонента намагниченности
. Предположим, что в какой-то момент времени компонента намагниченности 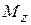 не равна своему равновесному значению
не равна своему равновесному значению 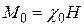 . Мы можем предположить (и это предположение оказывается хорошим приближением к действительности), что восстановление намагниченности происходит по экспоненциальному закону в соответствии с дифференциальным уравнением
. Мы можем предположить (и это предположение оказывается хорошим приближением к действительности), что восстановление намагниченности происходит по экспоненциальному закону в соответствии с дифференциальным уравнением
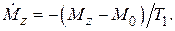 (10)
(10)
Здесь 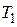 – характеристическая постоянная времени, иногда называемая временем “продольной релаксации”, поскольку она определяет изменения
– характеристическая постоянная времени, иногда называемая временем “продольной релаксации”, поскольку она определяет изменения 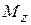 -компоненты, параллельной постоянному магнитному полю. Часто эту константу называют временем “спин-решёточной релаксации”, поскольку она связана с обменом энергией между спин-системой и решёткой, в которую внедрены диполи.
-компоненты, параллельной постоянному магнитному полю. Часто эту константу называют временем “спин-решёточной релаксации”, поскольку она связана с обменом энергией между спин-системой и решёткой, в которую внедрены диполи.
Взаимодействие двух одинаковых диполей в сильном поле Н может быть описано с классической точки зрения следующим образом. Первый диполь 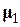 прецессирует с ларморовой частотой вокруг поля Н и, следовательно, обладает постоянной составляющей вдоль этого поля и составляющей, которая вращается в плоскости, перпендикулярной полю. Постоянная составляющая
прецессирует с ларморовой частотой вокруг поля Н и, следовательно, обладает постоянной составляющей вдоль этого поля и составляющей, которая вращается в плоскости, перпендикулярной полю. Постоянная составляющая 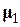 создаёт в месте расположения диполя
создаёт в месте расположения диполя 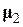 слабое постоянное поле (~
слабое постоянное поле (~ 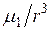 ), ориентация которого относительно Н зависит от взаимного расположения спинов. Поскольку Н – сильное поле, то на него заметно влияет только параллельная или антипараллельная ему составляющая слабого поля. Каждый спин в решётке имеет несколько соседей с различными относительными положениями и ориентациями, поэтому постоянная составляющая локального поля имеет разные значения в различных местах, что приводит к разбросу ларморовских частот и уширению линии резонансного поглощения. Вращающаяся составляющая
), ориентация которого относительно Н зависит от взаимного расположения спинов. Поскольку Н – сильное поле, то на него заметно влияет только параллельная или антипараллельная ему составляющая слабого поля. Каждый спин в решётке имеет несколько соседей с различными относительными положениями и ориентациями, поэтому постоянная составляющая локального поля имеет разные значения в различных местах, что приводит к разбросу ларморовских частот и уширению линии резонансного поглощения. Вращающаяся составляющая 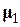 создает в месте расположения
создает в месте расположения 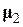 локальное магнитное поле, вращающееся с ларморовской частотой
локальное магнитное поле, вращающееся с ларморовской частотой 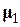 , которая совпадает с ларморовской частотой для
, которая совпадает с ларморовской частотой для 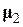 . В свою очередь она имеет составляющую в плоскости, перпендикулярной Н, и, следовательно, может заметно изменить ориентацию
. В свою очередь она имеет составляющую в плоскости, перпендикулярной Н, и, следовательно, может заметно изменить ориентацию 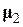 благодаря явлению резонанса. Соответствующая ширина линии должна быть порядка величины вращающегося поля. В рассматриваемом случае оно того же порядка величины, что и локальное постоянное поле, и, следовательно, вносит в уширение вклад сравнимой величины.
благодаря явлению резонанса. Соответствующая ширина линии должна быть порядка величины вращающегося поля. В рассматриваемом случае оно того же порядка величины, что и локальное постоянное поле, и, следовательно, вносит в уширение вклад сравнимой величины.
3. Здесь следует остановиться на различии между однородным и неоднородным уширениями. Линия считается неоднородно уширенной, если ширина обусловлена разбросом ларморовских частот различных магнитных моментов в образце. Причины такого разброса разнообразны – от неоднородности внешнего магнитного поля до локальных изменений гиромагнитного отношения g, вызванных взаимодействием диполей с их окружением. Какова бы ни была причина, неоднородное уширение имеет одну общую особенность: потеря фазовой когерентности, вызванная веерообразным расхождением индивидуальных прецессирующих диполей в плоскости xy, не является необратимой. Существует метод, известный под названием “спиновое эхо”, с помощью которого фазовая когерентность может быть восстановлена.
Если ширина линии в целом обусловлена релаксационными эффектами, то резонансная линия считается “однородно уширенной”. Прецессирующие компоненты дипольного поля индуцируют так называемые “флип-флоп” переходы, при которых один диполь теряет энергию, а другой приобретает её. Флип-флоп процесс наиболее эффективен тогда, когда диполи прецессируют с одинаковой частотой. При такой взаимной переориентации моментов суммарное значение 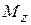 сохраняется, и полная энергия системы остаётся неизменной. Полные значения
сохраняется, и полная энергия системы остаётся неизменной. Полные значения 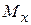 и
и 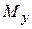 , напротив, не сохраняются; в результате переориентации спинов происходит постепенное разрушение фазовой когерентности между компонентами индивидуальных диполей в плоскости xy, и прецессирующая намагниченность в этой плоскости постепенно уменьшается до нуля. Флип-флоп процесс задаёт “истинное” время поперечной или спин-спиновой релаксации
, напротив, не сохраняются; в результате переориентации спинов происходит постепенное разрушение фазовой когерентности между компонентами индивидуальных диполей в плоскости xy, и прецессирующая намагниченность в этой плоскости постепенно уменьшается до нуля. Флип-флоп процесс задаёт “истинное” время поперечной или спин-спиновой релаксации 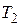 . Следуя Блоху, предположим, что компоненты намагниченности
. Следуя Блоху, предположим, что компоненты намагниченности 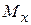 и
и 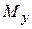 подчиняются дифференциальным уравнениям
подчиняются дифференциальным уравнениям
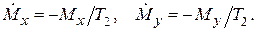 (11)
(11)
4. Как и раньше, мы предполагаем, что система спинов подвержена действию постоянного магнитного поля, направленного вдоль оси z, и поля 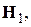 вращающегося с частотой w в плоскости xy и имеющего компоненты
вращающегося с частотой w в плоскости xy и имеющего компоненты 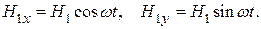 Распишем уравнение движения намагниченности (8):
Распишем уравнение движения намагниченности (8):
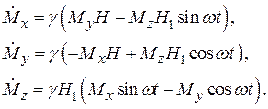 (12)
(12)
С учётом релаксационных эффектов они могут быть представлены в виде
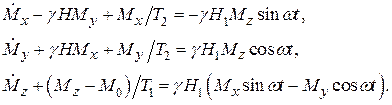 (13)
(13)
Впервые эти уравнения были даны Блохом. Нужно отметить, что в отличие от уравнения (10), действительного для любого агрегатного состояния вещества, уравнения (11) справедливы, строго говоря, только для магнитных моментов, находящихся в быстром движении друг относительно друга, т.е. для жидкостей и газов. Из уравнения (11) следует, что спад амплитуды поперечной намагниченности во времени происходит по экспоненциальному закону. Можно показать, что экспоненциальный спад поперечной намагниченности ~ 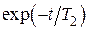 отвечает лоренцевой форме резонансной линии
отвечает лоренцевой форме резонансной линии
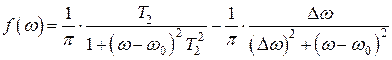 (14)
(14)
(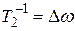 – ширина линии). Однако известно, что линии магнитного резонанса в твёрдых телах чаще всего имеют форму, близкую к гауссовой. Ниже мы получим решения уравнений движения намагниченности (13) для случая медленного прохождения через резонанс. Хотя эти решения нельзя считать адекватно описывающими магнитный резонанс в твёрдых телах, их можно использовать для анализа качественной стороны явления.
– ширина линии). Однако известно, что линии магнитного резонанса в твёрдых телах чаще всего имеют форму, близкую к гауссовой. Ниже мы получим решения уравнений движения намагниченности (13) для случая медленного прохождения через резонанс. Хотя эти решения нельзя считать адекватно описывающими магнитный резонанс в твёрдых телах, их можно использовать для анализа качественной стороны явления.
Будем искать стационарное решение, соответствующее вынужденной прецессии намагниченности вокруг постоянного магнитного поля с угловой скоростью приложенного поля 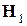 :
:
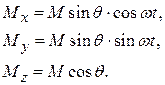 (15)
(15)
В дальнейшем удобно заменить поперечные компоненты 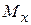 и
и 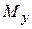 на
на
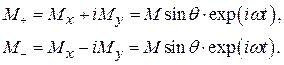 (16)
(16)
Предположим, что скорость прохождения через резонанс очень мала, и во все моменты времени преобладают стационарные условия: 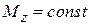 или
или 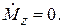 Тогда уравнения Блоха принимают такой вид:
Тогда уравнения Блоха принимают такой вид:
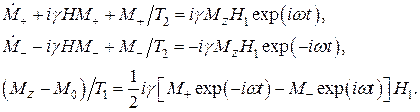 (17)
(17)
Имея в виду, что
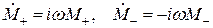 (см. (16)),
(см. (16)),
из первых двух уравнений (17) находим
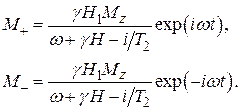 (18)
(18)
Подставив эти решения в третье уравнение Блоха (17), получаем выражение для продольной намагниченности 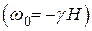 :
:
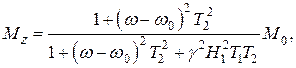 (19)
(19)
из которого видно, что компонента 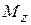 практически всегда равна
практически всегда равна 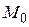 и даже при резонансе отличается от
и даже при резонансе отличается от 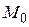 мало, если g 2 H 12 T 1 T 2 << 1. Комбинация (18) и (19) даёт выражение для компонент поперечной намагниченности:
мало, если g 2 H 12 T 1 T 2 << 1. Комбинация (18) и (19) даёт выражение для компонент поперечной намагниченности:
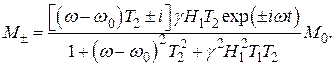 (20)
(20)
В целом, решения (19), (20) соответствуют прецессии вектора намагниченности вокруг поля Н под углом q к нему таким, что
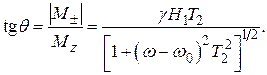 (21)
(21)
В большинстве экспериментов прохождение через резонанс осуществляется путём изменения поля Н, а частота w сохраняется при этом постоянной. Поэтому величину tg q удобно выразить через магнитные поля. Имея в виду, что 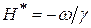 – резонансное поле для частоты w, а
– резонансное поле для частоты w, а 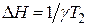 – ширина резонансной линии, мы можем переписать (21) в следующем виде:
– ширина резонансной линии, мы можем переписать (21) в следующем виде:
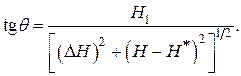 (22)
(22)
Обычно, при изучении магнитного резонанса стационарным методом амплитуда осциллирующего поля выбирается намного меньше ширины линии; поэтому угол q даже при резонансе близок к нулю.
Выясним, как ведёт себя при резонансе проекция намагниченности на плоскость, перпендикулярную постоянному полю Н. Угол, который составляет эта проекция с вектором осциллирующего поля 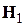 , можно найти из выражения
, можно найти из выражения
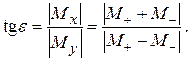 (23)
(23)
Подстановка (18) в (23) даёт:
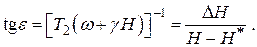 (23 a)
(23 a)
Таким образом, при прохождении резонанса ориентация вектора поперечной намагниченности относительно поля 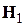 изменяется от параллельной до антипараллельной; при резонансе
изменяется от параллельной до антипараллельной; при резонансе 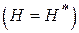 вектор поперечной намагниченности составляет с
вектор поперечной намагниченности составляет с 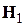 угол
угол 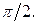
5. Осциллирующая часть намагниченности может быть выражена через комплексную восприимчивость:
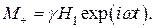 (24)
(24)
Пользуясь (24), запишем выражения для действительной и мнимой частей комплексной восприимчивости:
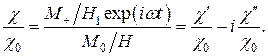 (25)
(25)
Подставив (20) в (25), получаем:
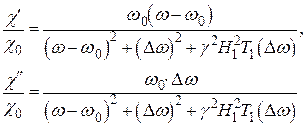 (26)
(26)
(в формулах (26) использовано обозначение 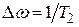 ).
).
Таким образом, действительная часть восприимчивости при резонансе равна нулю, а в стороне от резонанса она либо положительна (если 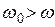 ), либо отрицательна (если
), либо отрицательна (если 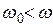 ). Мнимая часть восприимчивости при резонансе имеет максимум и, если
). Мнимая часть восприимчивости при резонансе имеет максимум и, если 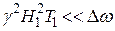 , то
, то
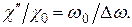 (27)
(27)
Это означает, что мнимая часть комплексной восприимчивости намного больше статической восприимчивости, если ширина линии мала по сравнению с резонансной частотой. Поэтому резонансные методы в 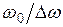 раз чувствительнее статических.
раз чувствительнее статических.
6. Выше отмечалось, что при выполнении условия 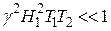 величина продольной компоненты намагниченности отличается от М 0 незначительно даже в момент резонанса. При резонансе величина
величина продольной компоненты намагниченности отличается от М 0 незначительно даже в момент резонанса. При резонансе величина
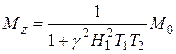 (28)
(28)
может оказаться малой только вследствие эффекта насыщения резонансной линии сильным радиочастотным полем 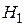 .Это происходит потому, что спин-система поглощает энергию осциллирующего поля с некоторой скоростью
.Это происходит потому, что спин-система поглощает энергию осциллирующего поля с некоторой скоростью 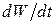 , и это поглощение повышает температуру спин-системы до тех пор, пока
, и это поглощение повышает температуру спин-системы до тех пор, пока 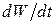 не сравняется со скоростью передачи энергии от спин-системы к решётке. Естественно, температура спин-системы возрастает с увеличением
не сравняется со скоростью передачи энергии от спин-системы к решётке. Естественно, температура спин-системы возрастает с увеличением 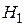 тем больше, чем длиннее времена спин-решёточной (
тем больше, чем длиннее времена спин-решёточной (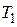 ) и спин-спиновой (
) и спин-спиновой (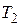 ) релаксаций.
) релаксаций.
7. Какова же скорость поглощения энергии радиочастотного поля спин-системой? Другими словами, какова поглощаемая мощность?
Имеем
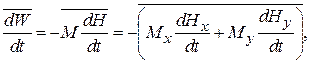 (29)
(29)
где 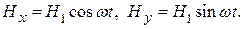
Подставив в (29) выражения для компонент поперечной намагниченности
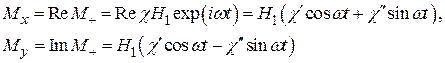 (30)
(30)
и произведя усреднение, получаем
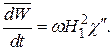 (31)
(31)
Таким образом, мощность, поглощаемая при резонансе, пропорциональна мнимой части комплексной восприимчивости. По этой причине эту величину 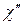 часто называют просто поглощением.
часто называют просто поглощением.
8. Частотная зависимость 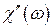 задаёт форму линии резонансного поглощения. В микроскопической теории показывается, что в общем случае мнимая часть комплексной восприимчивости связана со статической восприимчивостью соотношением
задаёт форму линии резонансного поглощения. В микроскопической теории показывается, что в общем случае мнимая часть комплексной восприимчивости связана со статической восприимчивостью соотношением
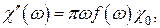 (32)
(32)
где 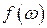 – так называемая функция формы линии, удовлетворяющая условию нормировки:
– так называемая функция формы линии, удовлетворяющая условию нормировки:
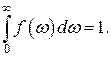 (33)
(33)
При подходящем выборе функции формы линии 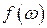 выражение (32) подобно выражению (27), полученному нами из макроскопических уравнений. Действительно, формулу (27) легко получить из формулы (32), подставив в последнюю лоренцеву функцию формы (14).
выражение (32) подобно выражению (27), полученному нами из макроскопических уравнений. Действительно, формулу (27) легко получить из формулы (32), подставив в последнюю лоренцеву функцию формы (14).
9. В выражении (32), как мы видим, отсутствуют квантово-механические величины. Это является следствием так называемых соотношений Крамерса-Кронига, которые связывают действительную и мнимую части комплексной восприимчивости. Вывод этих соотношений приведен в монографии [1]. В применении к нашей задаче соотношения Крамерса-Кронига могут быть представлены в виде
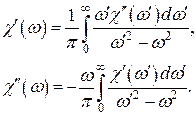 (34)
(34)
Из первого соотношения следует, что статическая магнитная восприимчивость равна
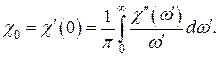 (35)
(35)
Действительно, подставив в (35) мнимую часть восприимчивости из (32), получаем
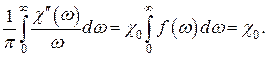
Здесь следует отметить, что формулы (26) для 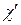 и
и 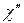 , полученные нами из макроскопических уравнений движения намагниченности, содержат члены с
, полученные нами из макроскопических уравнений движения намагниченности, содержат члены с 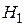 и удовлетворяют соотношениям Крамерса-Кронига только в предельном случае малых
и удовлетворяют соотношениям Крамерса-Кронига только в предельном случае малых 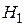 . При больших амплитудах
. При больших амплитудах 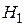 наступает насыщение, температура спин-системы становится выше температуры кристаллической решётки, и намагниченность перестаёт быть линейной функцией
наступает насыщение, температура спин-системы становится выше температуры кристаллической решётки, и намагниченность перестаёт быть линейной функцией 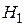 . Соотношения же Крамерса-Кронига справедливы только для линейных систем.
. Соотношения же Крамерса-Кронига справедливы только для линейных систем.
1.3. Диполь-дипольные взаимодействия в жёсткой решётке
Уширение резонансных линий обусловлено целым рядом физических причин. Самой простой из них является неоднородность приложенного постоянного магнитного поля. В обычных магнитах, создающих магнитные поля ~104 Гс, отклонение магнитного поля от среднего значения составляет несколько десятых долей гаусса; при помощи специальных сложных приспособлений это значение может быть снижено до нескольких миллигаусс. Однородность поля в пределах магнитного образца зависит от размеров образца. Обычно используются образцы, объёмы которых лежат в пределах от 0,1 см3 до нескольких кубических сантиметров.
Для ядер, обладающих электрическими квадрупольными моментами, может наблюдаться несколько резонансных линий. Появление таких линий связано с взаимодействием ядерного квадрупольного момента с электрическим полем кристалла. Это приводит к существенному уширению резонансных линий. Установление равновесных значений населённостей зеемановских уровней системы связано с переходами между этими уровнями под влиянием спин-решёточного взаимодействия. Благодаря таким переходам, время жизни системы на каком-либо одном уровне будет ограничено, что приводит к дополнительному уширению линии на величину 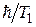 в энергетических единицах.
в энергетических единицах.
В этом разделе мы пренебрежём всеми перечисленными выше эффектами и сосредоточим внимание на механизме уширения резонансных линий, связанном с диполь-дипольным взаимодействием между магнитными моментами различных ядер. Такое пренебрежение во многих случаях вполне допустимо. В частности, оно вполне оправдано в тех случаях, когда спины отдельных ядер равны 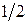 (в этом случае квадрупольные моменты ядер равны нулю), а время спин-решёточной релаксации достаточно велико.
(в этом случае квадрупольные моменты ядер равны нулю), а время спин-решёточной релаксации достаточно велико.
Вклад диполь-дипольных взаимодействий в ширину резонансных линий легко оценить по порядку величины. Если расстояние между соседними ядрами, обладающими магнитными моментами m, равно r, то каждое ядро будет создавать в точке, где находится соседнее ядро, магнитное поле 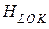 , по порядку величины равное
, по порядку величины равное
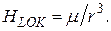 (36)
(36)
Если принять, что r = 2 Å и m = 10– 23 эрг/Гс (2 ядерных магнетона), то 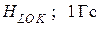 . Так как это поле может иметь различную ориентацию относительно постоянного поля
. Так как это поле может иметь различную ориентацию относительно постоянного поля 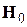 , резонансные частоты отдельных ядер будут распределены в области шириной примерно 1 Гс. В этой же области будет наблюдаться резонансное поглощение энергии. Из этих рассуждений следует, что ширина резонансной линии не зависит от внешнего магнитного поля Н.
, резонансные частоты отдельных ядер будут распределены в области шириной примерно 1 Гс. В этой же области будет наблюдаться резонансное поглощение энергии. Из этих рассуждений следует, что ширина резонансной линии не зависит от внешнего магнитного поля Н.
Классическое выражение для энергии взаимодействия двух магнитных моментов 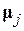 и
и 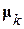 имеет следующий вид:
имеет следующий вид:
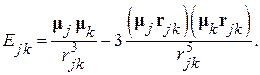 (37)
(37)
Для получения квантово-механического гамильтониана взаимодействия
необходимо подставить в (37) вместо векторов 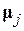 и
и 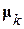 соответствующие операторы
соответствующие операторы
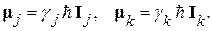 (38)
(38)
Полный гамильтониан системы N одинаковых взаимодействующих спинов в сильном внешнем магнитном поле может быть записан в виде
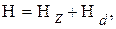 (39)
(39)
где
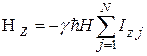 (40)
(40)
– энергия во внешнем магнитном поле, а
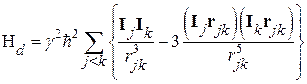 (41)
(41)
– энергия диполь-дипольного взаимодействия.
В дальнейшем, чтобы сделать формулы менее громоздкими, там, где это не может вызвать недоразумение, опустим индексы j и k сферических координат r, q, j. Тогда
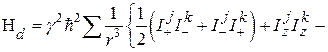
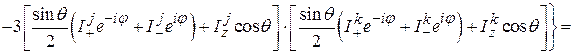
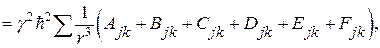 (42)
(42)
где
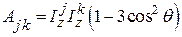 ,
,
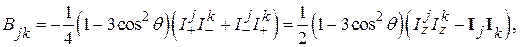
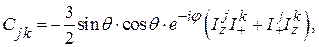
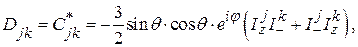 (43)
(43)
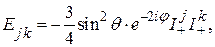
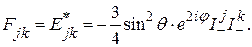
Рассмотрим взаимодействие j -ой и k -ой частиц. Допустим, что избрано такое представление, в котором z -компонента спина каждой частицы диагональна. Пусть 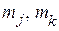 и М – квантовые числа проекций
и М – квантовые числа проекций 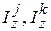 и
и 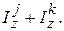 Нетрудно сообразить, что операторы (43) связывают состояния, различающиеся следующим образом:
Нетрудно сообразить, что операторы (43) связывают состояния, различающиеся следующим образом:
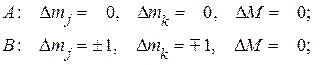
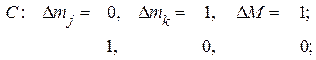
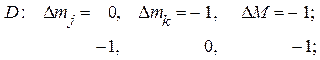
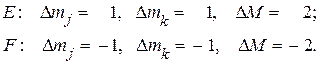
Мы видим, что матрицы А и В диагональны по М и коммутируют с матрицей зеемановской энергии (40).
Поскольку диполь-дипольное взаимодействие намного слабее зеемановского, естественно попытаться выяснить, какие заключения могут быть сделаны о спектре ЯМР и форме резонансных линий на основе теории возмущений. Рассмотрим энергетический уровень 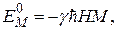 соответствующий гамильтониану(40). Этот уровень сильно вырожден, т.к. существует много способов, которыми можно скомбинировать отдельные значения
соответствующий гамильтониану(40). Этот уровень сильно вырожден, т.к. существует много способов, которыми можно скомбинировать отдельные значения 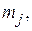 чтобы получить величину
чтобы получить величину 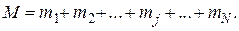
Возмущение, описываемое гамильтонианом H d, расщепляет уровень 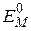 на много подуровней. Согласно первому приближению теории возмущений, вклад первого порядка в расщепление уровня
на много подуровней. Согласно первому приближению теории возмущений, вклад первого порядка в расщепление уровня 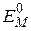 дают лишь те члены гамильтониана возмущения, которые обладают отличными от нуля матричными элементами внутри множества
дают лишь те члены гамильтониана возмущения, которые обладают отличными от нуля матричными элементами внутри множества 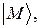 т.е. те, которые, действуя на состояние
т.е. те, которые, действуя на состояние 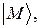 не вызывают изменения величины М. Обращаясь к (44), мы видим, что только операторы А и В удовлетворяют этому условию и должны быть сохранены для вычисления поправок к энергии
не вызывают изменения величины М. Обращаясь к (44), мы видим, что только операторы А и В удовлетворяют этому условию и должны быть сохранены для вычисления поправок к энергии 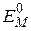 .
.
Член А имеет тот же вид, что и выражение для взаимодействия двух классических диполей, и описывает взаимодействие одного диполя со статическим локальным полем, создаваемым другим диполем.
Член В описывает взаимодействие, при котором возможно одновременное переворачивание двух соседних спинов в противоположных направлениях. Эта часть гамильтониана соответствует резонансному действию вращающегося локального поля.
Влияние члена С заключается в примешивании к состоянию 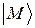 с невозмущённой энергией
с невозмущённой энергией 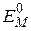 малой доли состояния
малой доли состояния 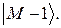 Таким образом, точное собственное состояние гамильтониана Hследует представить в виде
Таким образом, точное собственное состояние гамильтониана Hследует представить в виде 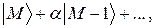 где
где 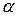 – малая величина порядка
– малая величина порядка 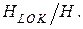
Под влиянием переменного магнитного поля между двумя зеемановскими уровнями 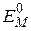 и
и 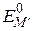 будут иметь место переходы с вероятностью, пропорциональной
будут иметь место переходы с вероятностью, пропорциональной
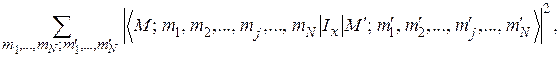 (45)
(45)
где 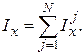
Из структуры матрицы 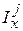 ясно, что
ясно, что 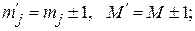 переходы
переходы
возможны только между соседними зеемановскими уровнями, что даёт одну резонансную линию на частоте 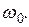
Этот вывод перестаёт быть справедливым, если перейти к следующему приближению теории возмущений. Действительно, с учётом операторов C, D, E и F правильные волновые функции можно представить в виде
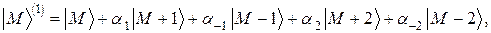 (46)
(46)
где 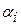 ~
~ 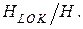 Теперь становятся возможными переходы
Теперь становятся возможными переходы 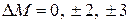 на частотах
на частотах 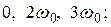 интенсивность дополнительных пиков поглощения пропорциональна
интенсивность дополнительных пиков поглощения пропорциональна 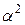 .
.
Матрица А + В такова, что её структура не изменится, если у диагональных элементов изменить знак на обратный. Поэтому решение векового уравнения А + В – Е = 0 даёт для энергии возмущения Е значения, которые попарно одинаковы по модулю, но различаются по знаку. Легко сообразить, что вероятности перехода между двумя парами подуровней, отличающихся знаками энергии, также будут одинаковы. Отсюда вытекает, что форма основной линии ЯМР симметрична относительно резонансной частоты.
Проведение детальных расчётов методом возмущений невозможно из-за огромного числа степеней свободы системы магнитных частиц. Поэтому широкое применение нашёл метод моментов, позволяющий учесть магнитные дипольные взаимодействия и оценить форму резонансной линии, не производя вычислений энергетического спектра. Анализ формы линий магнитного резонанса методом моментов впервые был выполнен Ван-Флеком.
1.4. Метод моментов и форма линии ЯМР
Важными характеристиками формы линий являются моменты линии. K -ый момент 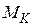 относительно частоты
относительно частоты 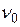 определяется следующей формулой:
определяется следующей формулой:
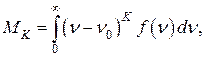 (47)
(47)
где 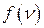 – функция формы линии.
– функция формы линии.
Положим 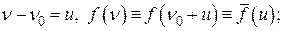
тогда 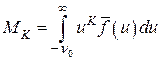 или для узких линий
или для узких линий
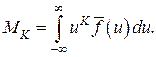 (48)
(48)
Разложим 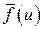 в интеграл Фурье:
в интеграл Фурье:
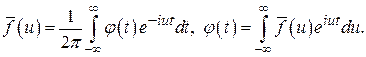 (49)
(49)
Фурье-образ 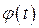 функции формы линии имеет простой физический смысл. Пусть ядерный парамагнетик находится в равновесном состоянии в постоянном магнитном поле Н, так что его намагниченность направлена по полю. Если на образец наложить короткий интенсивный импульс радиочастотного поля
функции формы линии имеет простой физический смысл. Пусть ядерный парамагнетик находится в равновесном состоянии в постоянном магнитном поле Н, так что его намагниченность направлена по полю. Если на образец наложить короткий интенсивный импульс радиочастотного поля 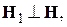 то под его воздействием намагниченность
то под его воздействием намагниченность 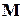 повернётся на некоторый угол a к полю Н. Допустим, что длительность импульса настолько мала, что можно пренебречь явлениями релаксации. Если бы резонансная линия была бесконечно узка, то после прекращения импульса намагниченность М совершала бы прецессию с частотой
повернётся на некоторый угол a к полю Н. Допустим, что длительность импульса настолько мала, что можно пренебречь явлениями релаксации. Если бы резонансная линия была бесконечно узка, то после прекращения импульса намагниченность М совершала бы прецессию с частотой 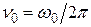 вокруг поля под постоянным углом a.
вокруг поля под постоянным углом a.
Эта свободная прецессия может быть детектирована по индуцированному ею сигналу в катушке, окружающей образец. Если ширина линии конечна, то вследствие разброса прецессионных частот сигнал затухнет за время порядка обратной ширины линии. Оказывается, что Фурье-образ функции формы линии просто связан с кривой затухания свободной прецессии: функция 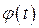 пропорциональна амплитуде сигнала свободной прецессии по окончании 900-импульса.
пропорциональна амплитуде сигнала свободной прецессии по окончании 900-импульса.
Разложим функцию 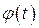 в ряд Тейлора вблизи точки
в ряд Тейлора вблизи точки 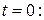
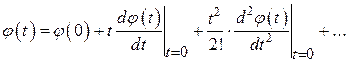 (50)
(50)
Из (49) вытекает, что
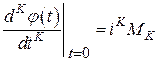 , (51)
, (51)
и, следовательно, если известны все моменты 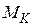 , то может быть восстановлена функция формы
, то может быть восстановлена функция формы 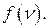 Существуют методы, позволяющие с большой точностью рассчитать моменты
Существуют методы, позволяющие с большой точностью рассчитать моменты 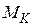 , однако с ростом К вычисления становятся настолько громоздкими, что приходится ограничиться расчётом лишь нескольких первых моментов. Поэтому для сопоставления теории с экспериментом пользуются несколькими типичными кривыми, из которых выбирают наиболее близкую к линии, полученной из опыта. Затем остаётся сравнить известные моменты типичной кривой с моментами, полученными теоретически.
, однако с ростом К вычисления становятся настолько громоздкими, что приходится ограничиться расчётом лишь нескольких первых моментов. Поэтому для сопоставления теории с экспериментом пользуются несколькими типичными кривыми, из которых выбирают наиболее близкую к линии, полученной из опыта. Затем остаётся сравнить известные моменты типичной кривой с моментами, полученными теоретически.
В качестве типичных кривых обычно пользуются следующими существенно различными функциями: гауссовой и лоренцевой.
У гауссовой линии
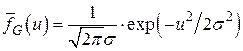 (52)
(52)
вершина более полога, а крылья спадают быстрее, чем у лоренцевой:
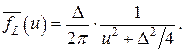 (53)
(53)
Ширина линии, определяемая равенством
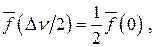 (54)
(54)
для гауссовой формы равна
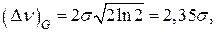
а для лоренцевой: 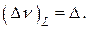
Для гауссовой линии чётные моменты равны
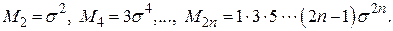 (55)
(55)
Для лоренцевой линии интегралы (48) при К > 1 расходятся. Поэтому лоренцеву линию обрезают на частотах 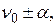 где a >>D/2.
где a >>D/2.
Тогда
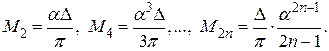 (56)
(56)
Гауссова и лоренцева линии симметричны относительно 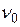 ; поэтому нечётные моменты равны нулю. Для того чтобы выяснить, насколько близка та или иная функция формы к гауссовой или лоренцевой линии, часто ограничиваются вычислениями отношения
; поэтому нечётные моменты равны нулю. Для того чтобы выяснить, насколько близка та или иная функция формы к гауссовой или лоренцевой линии, часто ограничиваются вычислениями отношения 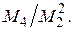 Для гауссовой линии
Для гауссовой линии
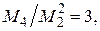 (57)
(57)
для лоренцевой линии
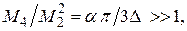 (58)
(58)
для линии прямоугольной формы 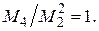
1.5. Вычисление моментов
Вернёмся к ширине и форме линии, уширенной благодаря диполь-дипольному взаимодействию. Наиболее простым, представляющим интерес, является второй момент дипольно уширенной линии, который в соответствии с (47) может быть определён как
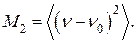 (59)
(59)
Из-за симметрии линии средняя частота 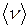 равна резонансной частоте
равна резонансной частоте 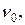 и поэтому
и поэтому
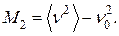 (60)
(60)
Пусть собственные значения гамильтониана H (39) суть 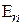 . Так как переход между уровнями
. Так как переход между уровнями 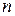 и
и 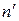 характеризуется частотой
характеризуется частотой
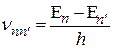
и интенсивностью, пропорциональной 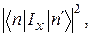 то
то
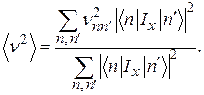 (61)
(61)
Легко показать, что эта формула может быть преобразована к виду
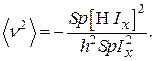 (62)
(62)
Действительно,
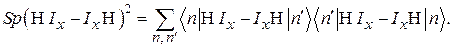
Так как след (шпур) матрицы инвариантен в отношении преобразования подобия, мы можем предположить, что матрица H диагональна, и тогда
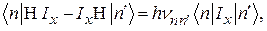
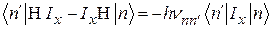
и, следовательно,
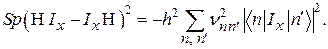
Знаменатель формулы (62) преобразуется следующим образом:
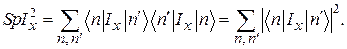
Справедливость формулы (62) доказана. Эта формула, в отличие от (61), очень удобна для расчётов, ибо следы матриц могут быть легко вычислены, в то время как нахождение собственных значений матриц при большом N связано с огромными трудностями.
Очень важно иметь в виду следующее. В формуле (62) учитывается поглощение на всех частотах 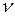 от 0 до ¥. Выше указывалось, что помимо главной резонансной линии на частоте
от 0 до ¥. Выше указывалось, что помимо главной резонансной линии на частоте 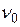 существуют дополнительные пики поглощения на частотах
существуют дополнительные пики поглощения на частотах 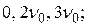 хотя эти пики слабы (они находятся далеко от центра основной линии), их вклад в моменты высокого порядка очень велик.
хотя эти пики слабы (они находятся далеко от центра основной линии), их вклад в моменты высокого порядка очень велик.
Поэтому, поскольку нас интересует только главная резонансная линия, в формуле (62) гамильтониан 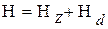 необходимо заменить “усечённым” гамильтонианом
необходимо заменить “усечённым” гамильтонианом 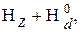 отбросив в операторе диполь-дипольного взаимодействия
отбросив в операторе диполь-дипольного взаимодействия 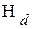 ту его часть, которая не коммутирует с
ту его часть, которая не коммутирует с 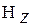 и поэтому приводит к появлению дополнительных резонансных пиков поглощения. Из (44) вытекает, что
и поэтому приводит к появлению дополнительных резонансных пиков поглощения. Из (44) вытекает, что
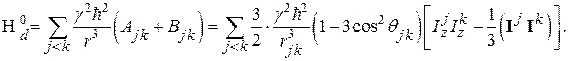 (63)
(63)
Детальные расчёты моментов сводятся к вычислениям следов из произведений спиновых матриц
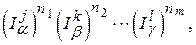
где 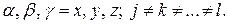 Полезно иметь в виду, что
Полезно иметь в виду, что
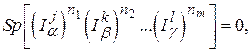 (64)
(64)
если хотя бы одна из степеней 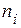 является нечётным числом.
является нечётным числом.
Воспользовавшись (64), нетрудно показать, что в (62) исчезают перекрёстные члены, содержащие произведения 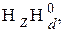 так что (62) переходит в следующую формулу:
так что (62) переходит в следующую формулу:
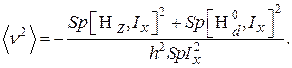 (65)
(65)
Если бы не было диполь-дипольных взаимодействий и 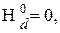 то, очевидно,
то, очевидно,
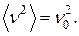 Из (60) и (65) получаем окончательно
Из (60) и (65) получаем окончательно
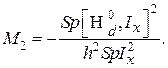 (66)
(66)
Аналогично, для четвёртого момента имеем
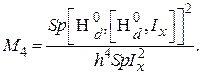 (67)
(67)
Вычисления (66) с гамильтонианом (63) дают следующее выражение для второго момента (формула Ван-Флека):
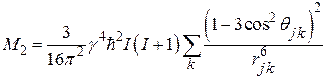 [Гц2]. (68)
[Гц2]. (68)
Для порошка, содержащего кристаллы с хаотическими ориентациями, это выражение упрощается благодаря исчезновению угловой зависимости. Усредняя по сфере, получаем 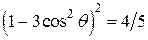 и, следовательно,
и, следовательно,
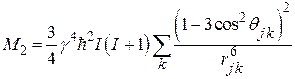 [(рад/с) 2],
[(рад/с) 2],
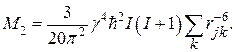 (69)
(69)
Для простой кубической решётки с постоянной 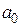 имеем
имеем
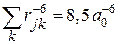
и
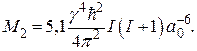 (70)
(70)
В случае монокристалла с простой кубической решёткой
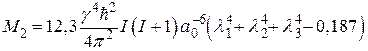 [Гц2], (71)
[Гц2], (71)
где 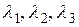 – направляющие косинусы внешнего поля относительно осей кристалла;
– направляющие косинусы внешнего поля относительно осей кристалла; 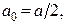 где
где 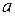 – постоянная решётки.
– постоянная решётки.
Заметим, что с учётом в гамильтониане диполь-дипольного взаимодействия только статической части
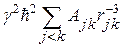
второй момент 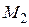 получается в
получается в 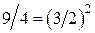 раз меньше. Если же, наоборот, мы включим в рассмотрение все операторы от A до F (см. (43)), то получим сильно завышенное значение. Простой расчёт показывает, что для порошка замена
раз меньше. Если же, наоборот, мы включим в рассмотрение все операторы от A до F (см. (43)), то получим сильно завышенное значение. Простой расчёт показывает, что для порошка замена 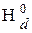 на полный гамильтониан
на полный гамильтониан 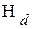 приводит к увеличению
приводит к увеличению 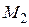 в
в 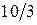 раз.
раз.
Зная только 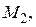 нельзя сделать выводы относительно формы резонансной линии. Поэтому, используя выражение (67), целесообразно вычислить ещё, по крайней мере, четвёртый момент. Результат этого громоздкого вычисления можно представить в виде:
нельзя сделать выводы относительно формы резонансной линии. Поэтому, используя выражение (67), целесообразно вычислить ещё, по крайней мере, четвёртый момент. Результат этого громоздкого вычисления можно представить в виде:
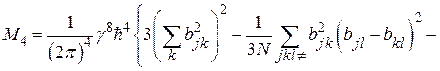
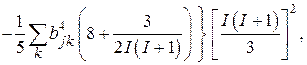 (72)
(72)
где
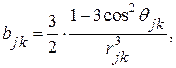
а символ 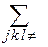 означает, что в тройном суммировании не должно быть двух одинаковых индексов. Численная оценка (72) затруднительна даже для простой кубической решётки, если направление магнитного поля относительно кристаллографических осей произвольно. Если сохранить в фигурных скобках только первый член, то
означает, что в тройном суммировании не должно быть двух одинаковых индексов. Численная оценка (72) затруднительна даже для простой кубической решётки, если направление магнитного поля относительно кристаллографических осей произвольно. Если сохранить в фигурных скобках только первый член, то 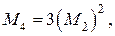 что отвечает гауссовой форме линии.
что отвечает гауссовой форме линии.
 2015-06-26
2015-06-26 988
988








