Локальна теорема Лапласа. Ймовірність того, що в 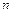 незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює
незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює 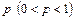 , подія настане рівно
, подія настане рівно 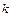 разів (байдуже, в якій послідовності), наближено дорівнює
разів (байдуже, в якій послідовності), наближено дорівнює
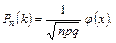
Тут
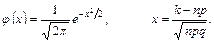
Функція 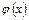 для додатних значень
для додатних значень 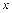 табульована (наведена у таблиці); для від’ємних значень
табульована (наведена у таблиці); для від’ємних значень 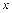 користуються цією ж таблицею [функція
користуються цією ж таблицею [функція 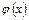 парна, отже,
парна, отже, 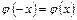 ].
].
Інтегральна теорема Лапласа. Ймовірність того, що 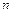 в незалежних випробуваннях, у кожному з яких імовірність появи події дорівнює
в незалежних випробуваннях, у кожному з яких імовірність появи події дорівнює 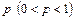 , подія настане не менше
, подія настане не менше 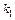 разів і не більше
разів і не більше 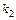 разів, наближено дорівнює
разів, наближено дорівнює
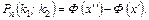
Тут
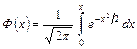
– функція Лапласа,
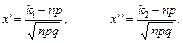
Функція Лапласа 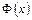 для додатних значень
для додатних значень 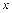
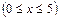 табульована (наведена у таблиці); для значень
табульована (наведена у таблиці); для значень 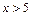 вважають
вважають 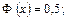 для від’ємних значень
для від’ємних значень 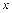 користуються цією ж таблицею, враховуючи, що функція Лапласа непарна
користуються цією ж таблицею, враховуючи, що функція Лапласа непарна 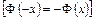 .
.
Відхилення відносної частоти від постійної ймовірності
в незалежних випробуваннях
Оцінка відхилення відносної частоти від постійної ймовірності. Ймовірність того, що в 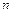 незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює
незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює 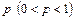 , абсолютна величина відхилення відносної частоти появи події від ймовірності появи події не перевищить додатного числа
, абсолютна величина відхилення відносної частоти появи події від ймовірності появи події не перевищить додатного числа 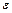 , наближено дорівнює подвоєній функції Лапласа при
, наближено дорівнює подвоєній функції Лапласа при 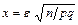 :
:
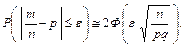
Найімовірніше число появ події
в незалежних випробуваннях
Найімовірніше число настання події. Число 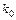 (настання події в незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює
(настання події в незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює 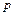 ) називають найімовірнішим, якщо ймовірність того, що подія настане в цих випробуваннях
) називають найімовірнішим, якщо ймовірність того, що подія настане в цих випробуваннях 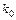 разів, перевищує (або, принаймні, не менше) ймовірності інших, можливих результатів випробувань.
разів, перевищує (або, принаймні, не менше) ймовірності інших, можливих результатів випробувань.
Найімовірніше число 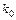 визначається з подвійної нерівності
визначається з подвійної нерівності
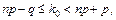
причому:
а) якщо число 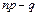 – дробове, то існує одне найімовірніше число
– дробове, то існує одне найімовірніше число 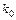 ;
;
б) якщо число 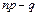 – ціле, то існує два найімовірніших числа, а саме:
– ціле, то існує два найімовірніших числа, а саме: 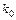 і
і 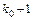 ;
;
в) якщо число 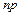 – ціле, то найімовірніше число
– ціле, то найімовірніше число 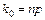 .
.
 2015-06-26
2015-06-26 1344
1344
