Уравнение прямой, проходящей черед две данные точки 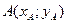 и
и 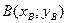 , имеем вид
, имеем вид
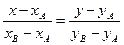 . (1)
. (1)
Если точки А и В определяют прямую, параллельную оси 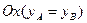 или оси
или оси 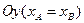 , то уравнение такой прямой записывается в соответственно в виде
, то уравнение такой прямой записывается в соответственно в виде
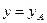 или
или 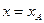 .
.
Задача. Составить уравнение прямой, проходящей через точки 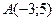 и
и 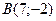 .
.
Решение. Воспользуемся уравнением (1):
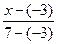 =
= 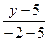 , или
, или 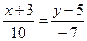 ,
,
Откуда
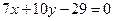 .
.
Задача. Проверить, лежат ли точки 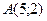 ,
, 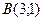 и
и 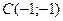 на одной прямой.
на одной прямой.
Решение. Составим уравнение прямой, проходящей через точки 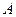 и
и 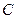 :
:
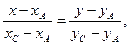 или
или 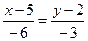 .
.
Подставляя в это уравнение координаты точки 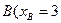 и
и 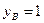 ), получим
), получим 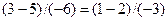 , т.е.
, т.е. 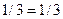 . Таким образом, координаты точки
. Таким образом, координаты точки 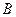 удовлетворяют уравнению прямой
удовлетворяют уравнению прямой 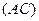 , т.е.
, т.е. 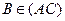 .
.
 2015-06-28
2015-06-28 1055
1055
