Уравнением прямой в отрезках называется уравнение вида
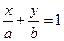 , (1)
, (1)
Где a и b – абсцисса и ордината точек пересечения прямой с осями 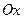 и
и 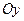 , то есть длины отрезков, отсекаемые прямой на координатных осях, взятые с соответствующими знаками.
, то есть длины отрезков, отсекаемые прямой на координатных осях, взятые с соответствующими знаками.
Задача. Общее уравнение прямой 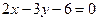 привести к уравнению в отрезках.
привести к уравнению в отрезках.
Решение. Запишем данное уравнение в виде 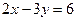 и разделим обе его части на свободный член:
и разделим обе его части на свободный член:
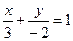 .
.
Это и есть уравнение данной прямой в отрезках.
Задача. Через точку 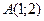 , провести прямую, отсекающую на положительных полуосях координат равные отрезки.
, провести прямую, отсекающую на положительных полуосях координат равные отрезки.
Решение. Пусть уравнение искомой прямой имеет виде 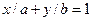 . По условию
. По условию 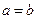 . Следовательно, уравнение прямой принимает вид
. Следовательно, уравнение прямой принимает вид 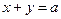 . Так как точка с координатами
. Так как точка с координатами 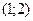 принадлежит этой прямой, то числа
принадлежит этой прямой, то числа 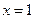 ,
, 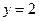 удовлетворяют уравнению
удовлетворяют уравнению 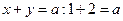 , откуда
, откуда 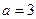 .
.
Итак, искомое уравнение записывается следующим образом:
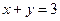 , или
, или 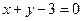 .
.
 2015-06-28
2015-06-28 3241
3241
