Параболой называется множество точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.
Тогда уравнение параболы примет вид:
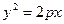 ;
;
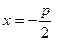 уравнение директрисы
уравнение директрисы 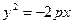 ;
;
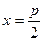 уравнение директрисы
уравнение директрисы

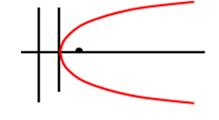

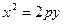 ;
; 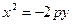 ;
;
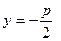 уравнение директрисы
уравнение директрисы 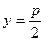 уравнение директрисы
уравнение директрисы
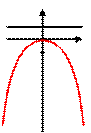

Задача. Определить координаты фокуса и составить уравнение директрисы параболы 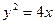 .
.
Решение. Сравнивая это уравнение с уравнением (1), находим, что 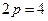 , откуда
, откуда 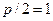 . Таким образом, точка
. Таким образом, точка 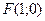 - фокус параболы, а прямая
- фокус параболы, а прямая 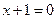 - ее директриса.
- ее директриса.
Задача. Составить уравнение параболы с вершиной в начале координат и фокусом в точке 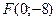 .
.
Решение. Фокус параболы лежит на оси ординат, а вершина – в начале координат, поэтому уравнение параболы можно записать либо в виде 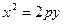 , либо в виде
, либо в виде 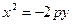 . Далее, поскольку ордината фокуса отрицательна, уравнение параболы следует искать в виде
. Далее, поскольку ордината фокуса отрицательна, уравнение параболы следует искать в виде 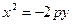 . Фокусное расстояние параболы
. Фокусное расстояние параболы 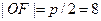 , откуда
, откуда 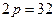 и окончательно получаем
и окончательно получаем 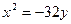 .
.
Задача. Показать, что уравнение

Представляет собой уравнение параболы.
Решение. Приведем данное уравнение к простейшему виду. Для этого выразим y через x и в полученном выражении выделим полный квадрат:
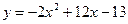 , или
, или 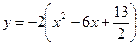 ,
,
Т.е.
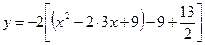 ,
,
Откуда
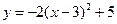 .
.
Следовательно,
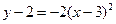 , или
, или 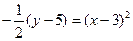 .
.
 2015-06-28
2015-06-28 1114
1114