Определение 11. Квадратная матрица (т = п) называется вырожденной, если ее определитель равен нулю, и невырожденной в противном случае.
Определение 12. Если А - невырожденная матрица, то существует, и притом единственная, матрица 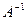 такая, что
такая, что
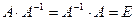 ,
,
где Е - единичная матрица того же размера, что и матрицы А и А-1.
Матрица А-1 называется обратной к матрице А.
Определение 13. Назовем матрицу АT транспонированной, если она является транспонированной матрицей, составленной из алгебраических дополнений соответствующих элементов матрицы А.
Если матрица А — невырожденная, то
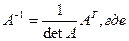
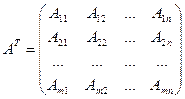
Пример 2. Найти сумму матриц А и В, если
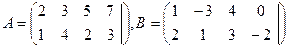
Решение.
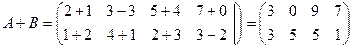
Ответ 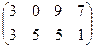
Пример 3. Вычислить матрицу 2А+ 5В, если
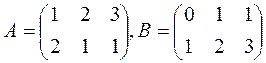
Решение.
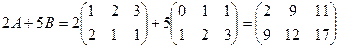
Ответ 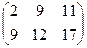
Пример 4. Найти произведение АВ матрицы-строки А = (5 7 -2) на матрицу
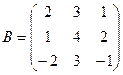
Решение.
(5 7-2) 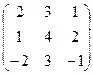 =
= 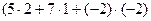
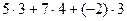
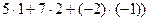 = = (21 37 21).
= = (21 37 21).
Ответ: матрица-строка размера (1x3)- (21 37 21).
Замечание. (1x3)- матрица при умножении на (3 х 3) - матрицу дает (1x3)- матрицу.
Пример 5. Найти произведение АВ, если А = 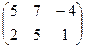
- (2 х 3) - матрица, В = 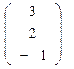 -(3x1)- матрица.
-(3x1)- матрица.
Решение. При умножений (2 х 3) - матрицы на (3 х 1) матрицу получим (2x1) — матрицу.
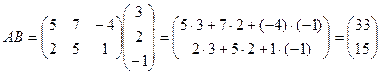
Ответ 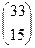
Пример 6. Даны матрицы 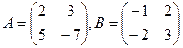 Найти матрицы АВ и ВА.
Найти матрицы АВ и ВА.
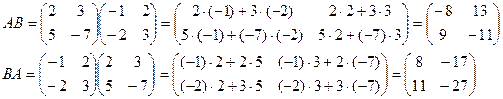
Ответ: 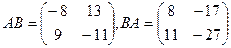
Замечание. Очевидно, АВ≠ ВА, т.е. произведение матриц не перестановочно.
Пример 7. Доказать, что матрица 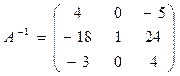
является обратной для матрицы 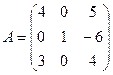
Решение. 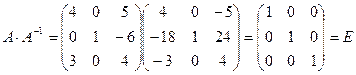
Ответ: матрица А-1 является обратной матрице А.
Пример 8. Найти транспонируемую матрицу для матрицы
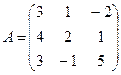
Решение.
Присоединенная матрица является транспонированной матрицей из алгебраических дополнений данной матрицы.
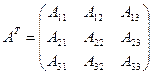 -
-
Для данной матрицы 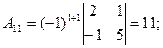
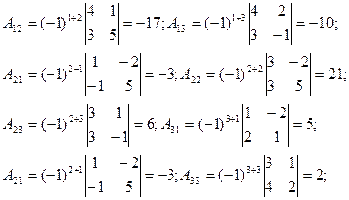
Итак, транспонируемая матрица АТ равна
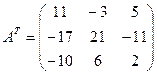
Пример 9. Найти матрицу А-1, обратную к матрице А примера 8.
Решение. Так как 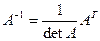 , то найдем
, то найдем
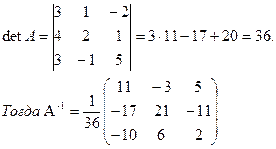
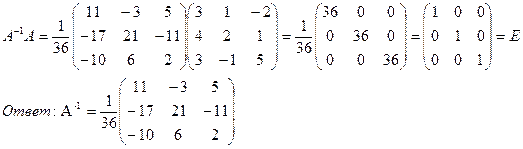
 2015-06-28
2015-06-28 2110
2110
