2015-06-28
2426
Примеры:
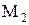- множество всех натуральных чисел (N).
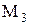- множество всех решений уравнения 
.
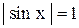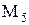- множество всех действительных чисел.
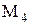- множество всех чисел 
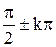, где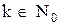 
можно интерпретировать как описание свойства его элементов, заключающегося в возможности представить их в виде .
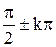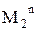- заданное как “множество всех целых чисел, являющихся степенью двойки”, 
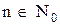. Такой способ задания множества применяется, когда свойство элементов М может быть описано коротким выражением. Например, P(x) читается: «х обладает свойством Р», то М задается при помощи обозначения 
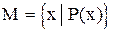читается: «М - множество элементов х, обладающих свойством Р».
Пример:
1) 
.
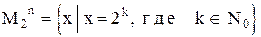2) 
.
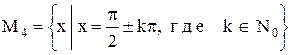Требования к описанию свойств - точность и недвусмысленность.
Пример:
Множество всех красивых первокурсниц математического факультета 2002 г. не строго определено, так как у разных людей – различные критерии отбора.
Надежный способ точно описать свойства элементов данного множества - задание распознающей (разрешающей) процедуры, которая для любого объекта устанавливает, обладает он свойством или нет (т. е. является элементом множества или нет).
|
|
|
Пример:
Для 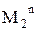, то есть для свойства, быть степенью двойки разрешающей процедурой является любой метод разложения целых чисел на простые множители. Здесь разрешающая процедура не является порождающей. Но ее нетрудно таковой сделать: например, порождающая процедура может быть таковой. Берем последовательно все натуральные числа и каждые из них разлагаем на простые множители: те числа, которые не содержат множителей, отличных от двойки, включаем в .
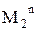С другой стороны порождающая процедура может не быть разрешающей. Например, при получении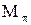 
действует порождающая процедура. Но с ее помощью нельзя определить, будет ли произвольное трехзначное число принадлежать 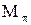или нет, т. е. множество 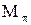бесконечно, и если при построении n - чисел множества некоторое (проверяемое) число не встретилось, то еще нельзя утверждать, что оно не принадлежит .
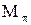Обобщение: Суть порождающей процедуры в том, что с ее помощью из уже полученных элементов множества или других объектов получают (или могут получить) все последующие элементы.
Суть разрешающей процедуры в том, что она разрешает (или не разрешает) предложенному для проверки объекту быть или не быть элементом данного множества в зависимости от его свойств.
Понятие “точно заданное множество” нуждается в уточнении. Одна из основных трудностей задания множества (даже из множеств, точность описания которых не вызывает сомнения) с помощью вполне, казалось бы, законных средств - в том, что можно сконструировать описание множеств, которые приводят к противоречиям - “парадоксам теории множеств”. Например, множество всех подмножеств по смыслу своего описания этого множества должно содержать все мыслимые множества. Но оно само содержится в множестве своих подмножеств в качестве элемента.
|
|
|
Перед дальнейшим изложением будет удобно определить два специальных множества.
Определение: Пустое множество (обозначается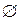 
) есть множество, обладающее свойством:
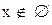при любом х.
Другое множество, определение которого зависит от задачи, называют универсальным множеством.
Определение: Универсальное множество (обозначается U) есть множество всех рассматриваемых в данной задаче элементов.
Рассмотрим теперь множество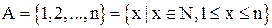 
. Оно имеет n элементов. Будем говорить, что мощность этого множества есть n.
Определение: Мощностью (длиной, размерностью) множества называется число элементов этого множества. Обозначим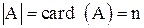 
.
Далее любое множество В, которое имеет то же число элементов, что и А, имеет такую же мощность, и естественно, эти элементы не надо пересчитывать. Для небольших множеств достаточно легко пересчитать элементы, но для других множеств, например N, это может быть невозможно. Далее следует строгое, но неформальное определение количества элементов.
Определение: Говорят, что множество Х конечно, если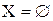 
или для некоторого 
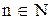существует множество 
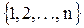такое, что оно имеет то же самое число элементов, что и X. Если 
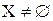и никакого n не может быть найдено, то Х называют бесконечным.
