Скалярное произведение Основные понятия и определения

Определение 25.

Скалярным произведением двух векторов и 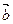называется число, равное произведению модулей этих векторов на косинус угла между ними

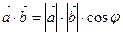(8.1)

Из определения следует:

1) 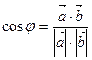(2), где 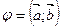– угол между и .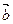

2) условие перпендикулярности двух ненулевых векторов: если векторы перпендикулярны (ортогональны), то 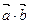=0

Свойства скалярного произведения векторов:

1. 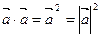. Скалярный квадрат вектора равен квадрату его модуля.

Доказательство по определению (самостоятельно)

2. 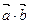= 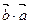. Скалярное произведение коммутативно.

Доказательство по определению (самостоятельно)

3. 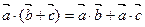. Для скалярного произведения справедлив дистрибутивный закон.

Доказательство по определению (самостоятельно)

4. 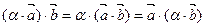. Для скалярного произведения справедлив сочетательный закон относительно скалярного множителя.

Доказательство по определению (самостоятельно)

5. Если 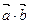=0, то угол 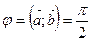, если 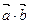>0, то угол 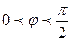, если 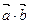<0, то угол .

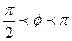6. 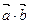= 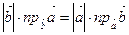. (8.2)

Доказательство по определениям скалярного произведения и проекции вектора на вектор (самостоятельно)