2015-06-28
806
Рассмотрим двумерное векторное пространство V 2. Выделим в нем два подпространства: положительно ориентированное (против часовой стрелки) и отрицательно ориентированное (по часовой стрелке). Подпространство, в котором выбрана положительная ориентация, назовем просто ориентированным.
Рассмотрим трехмерное векторное пространство V 3. По аналогии с ориентацией плоскости выделим в нем два подпространства: положительно ориентированное и отрицательно ориентированное. Положительно ориентированный в нем базис назовем правым, отрицательно ориентированный соответственно – левым.
Рассмотрим три некомпланарных вектора 
, 
, 
(порядок определен строго).
Определение 28.
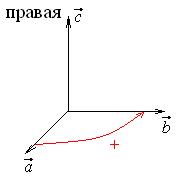
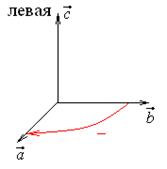
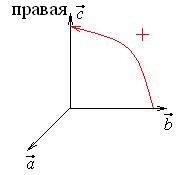
Три вектора , , образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму совершается против часовой стрелки.
Примеры.
1) , , 2) , , 3) , ,
