Из свойства 1 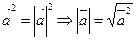 , в координатах по формуле (8.3):
, в координатах по формуле (8.3):
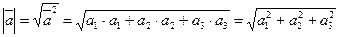
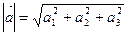 (8.4)
(8.4)
Пусть длины векторов: 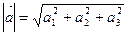 ,
, 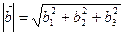 , Из определения и формул (8.3)-(8.4) следует, что угол между векторами вычисляется по формуле:
, Из определения и формул (8.3)-(8.4) следует, что угол между векторами вычисляется по формуле:
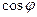 =
= 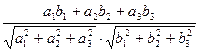 . (8.5)
. (8.5)
Пример 1. Вычислим косинус угла между ребрами АВ и СD тетраэдра DАВС, если А (1;2;1), В (4;1;2), С (1;5;3), D (2;3;1).
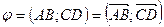 . Найдем координаты векторов
. Найдем координаты векторов 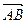 и
и 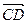 :
:
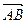 (4–1;1–2;2–1),
(4–1;1–2;2–1), 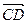 (2–1;3–5;1–3), тогда
(2–1;3–5;1–3), тогда 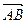 (3;–1;1),
(3;–1;1), 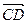 (1;–2;–2).
(1;–2;–2).
Подставим в формулу и вычислим:
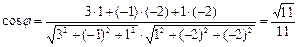 ,
, 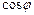 »0,3015 (т.е. j»72о).
»0,3015 (т.е. j»72о).
Определение 26.
Ортом вектора 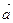 называется вектор
называется вектор 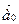 , который имеет единичную длину и то же направление, что и вектор
, который имеет единичную длину и то же направление, что и вектор 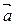 .
.
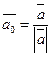 (8.6)
(8.6)
Процесс получения орта вектора называется нормированием.
Если координаты 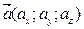 , то координаты соответствующего вектору орта, т.е. нормированного вектора,
, то координаты соответствующего вектору орта, т.е. нормированного вектора,
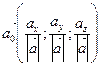 . (8.7)
. (8.7)
Направление вектора определяется углами α, β, γ, образованными вектором с осями координат Ox, Oy, Oz.
Определение 27.
Косинусы углов α, β, γ, образованных векторов с осями координат Ox, Oy, Oz, называются направляющими косинусами вектора и вычисляются по формулам:
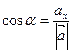 ,
, 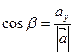 ,
, 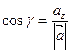 . (8.8)
. (8.8)
Тогда координаты нормированного вектора по (8.8) в V 3 будут:
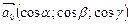 .
.
Направляющие косинусы вектора связаны соотношением 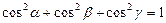 .
.
Для V 2: 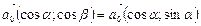 с соотношением:
с соотношением: 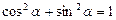 .
.
 2015-06-28
2015-06-28 1489
1489
