Пусть 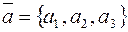 ,
, 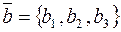 и
и 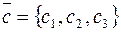 . Тогда
. Тогда
по определению имеем:
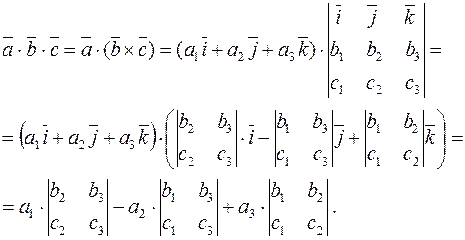
В полученном выражении легко увидеть разложение определителя, составленного из проекций перемножаемых векторов. Итак, имеем формулу, выражающую смешанное произведение трех векторов через проекции сомножителей:
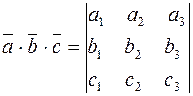 .
.
IV Условие компланарности векторов
Векторы 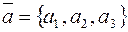 ,
, 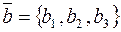 и
и 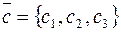 компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е.
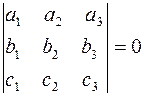 .
.
Действительно, если 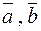 и
и 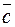 компланарные, то
компланарные, то  лежит в плоскости векторов
лежит в плоскости векторов 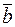 и
и 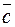 , а вектор
, а вектор 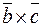 перпендикулярен этой плоскости (по определению векторного произведения). Но тогда,
перпендикулярен этой плоскости (по определению векторного произведения). Но тогда, 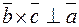 , а значит
, а значит 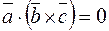 .
.
С другой стороны, если определитель равен нулю, то одна из его строк есть линейная комбинация двух других, т.е. один из векторов есть линейная комбинация двух других, а значит лежит в плоскости этих двух векторов (заметим, что все векторы считаются приведенными к общему началу).
Пример. Даны вершины тетраэдра A (3;2;1), B (1;4;–2), C (3;6;–7)
и D (–4;–5;8). Найти его объём и длину высоты, опушенной из вершины D.
Решение. Найдем векторы, идущие из вершины А тетраэдра по его ребрам:
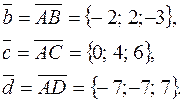
Найдем смешанное произведение этих векторов
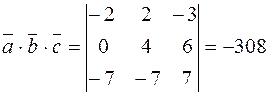 .
.
Объем параллелепипеда, построенного на  равен
равен 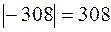 (знак “–“ говорит о том, что эта тройка векторов левая). Объем тетраэдра, построенного на трех векторах, составляет одну шестую часть объема параллелепипеда, построенного на тех же векторах. Итак, искомый объем равен
(знак “–“ говорит о том, что эта тройка векторов левая). Объем тетраэдра, построенного на трех векторах, составляет одну шестую часть объема параллелепипеда, построенного на тех же векторах. Итак, искомый объем равен 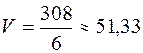 . С другой стороны,
. С другой стороны,
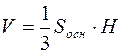 ,
,
оттуда 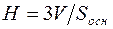 . Площадь же основания найдем как половину модуля векторного произведения соответствующих векторов: если высота опускается из вершины D, то основание – это ΔАВС. Находим векторное произведение:
. Площадь же основания найдем как половину модуля векторного произведения соответствующих векторов: если высота опускается из вершины D, то основание – это ΔАВС. Находим векторное произведение:
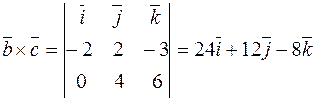 .
.
Тогда
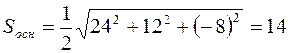 .
.
Итак,
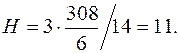
 2015-06-28
2015-06-28 1026
1026