Примеры. · Алгебра (R; +, ·) называется полем действительных чисел

· Алгебра (R; +, ·) называется полем действительных чисел. Обе операции – бинарные, поэтому тип этой алгебры – <2,2>. Все конечные подмножества R, кроме {0}, не замкнуты относительно обеих операций. Подалгеброй этой алгебры является, например, поле рациональных чисел.

· Пусть N_p={0,1,2, …, p-1}. Определим на N_p операцию Å («сложение по модулю р») и Ä («умножение по модулю р») следующим образом: aÅb=c, aÄb=d, где c и d – остатки от деления на р чисел a+b и ab. Например, если р=7, то N_p={0,1,2, …, 6}, 3Å4=0, 3Ä4=5 и т.д. Часто эти операции обозначают как a+b≡c(modp), ab≡d(modp). Если р – простое число, то алгебра (N_p; Å, Ä) называется конечным полем характеристики р или полем Галуа и обозначается GF(p).

· Операции поля Галуа для р=3 (троичной арифметики) можно задать с помощью таблиц Кэли (см. ранее).

· Пусть задано множество U. Алгебра B=(2^U; <Ç, ∩, \, Δ, ‾, ¯, U>) называется булевой алгеброй множеств над U, её тип <2,2,2,2,1,0,0> (или <2,2,1>), носителем является множество всех подмножеств множества U (булеан), сигнатура состоит из следующих операций: бинарные Ç, ∩, \, Δ, унарная ‾ (дополнение), и нульарные (фиксированные элементы 2^U) U и ¯.

· Для произвольного множества М можно определить алгебру (2^М‰М; <Ç, •, ^-1,>) типа <2,2,1>, носителем которой является множество всех подмножеств декартова квадрата множества М, а сигнатура состоит из операций объединения и композиции бинарных отношений на М, обратное отношение к данному – унарная операция ^–1.

· {R; ↑n: n>1} возведение в степень, тип – <2,3,…> – счётная сигнатура.

· Множество F одноместных функций на R, т.е. функций f: R→R вместе с операцией дифференцирования является алгеброй: {{f| f: R→R}; d/dx}. Носителем служит множество функций типа R→R, единственной операцией этой алгебры служит дифференцирование – унарная операция F→F (производной функции на R является снова функция на R). Множество элементарных функций замкнуто относительно дифференцирования, поскольку производные элементарных функций элементарны и, следовательно, образуют подалгебру данной алгебры.

· Рассмотрим квадрат с вершинами в точках а₁, а₂, а₃, а₄, пронумерованных против часовой стрелки, и повороты квадрата вокруг центра в том же направлении, переводящего вершины в вершины. Таких поворотов бесконечно много: на углы 0, π/2, π, 3π/2, 2π, 5π/2…, однако они задают всего четыре различных отображения множества вершин в себя, соответствующее первым четырём поворотам.

Таким образом, получаем алгебру с основным множеством { а₁, а₂, а₃, а₄} и четырьмя унарными операциями α, β, γ, δ. Их можно задать Таблицей 1, в которой на пересечении, например, строки а₃ и столбца γ написано значение функции γ(а₃). Операция α, отображающая любой элемент в себя, называется тождественной операцией. Она соответствует нулевому повороту. Подалгебр в этой алгебре нет.

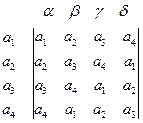
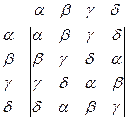
Таблица 1 Таблица 2

Множество О={α, β, γ, δ} отображений вершин в себя вместе с бинарной операцией композиции отображений 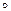образует алгебру (O, 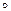). Элементами множества О являются отображения (повороты).

Композиция отображений – это последовательное выполнение двух поворотов. Она задаётся Таблицей 2 (в ней на пересечении строки α и столбца β написан результат композиции α 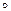β). Это снова таблица Кэли. Множество {α, γ} т.е. повороты на углы 0, π образуют подалгебру алгебры (O, ).

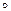Конечной алгеброй называется алгебра с конечным носителем.

Свойства операций в определение алгебры не входят. Их обычно указывают дополнительно, говоря: коммутативная алгебра, ассоциативная алгебра, алгебра с нулём и единицей.

Нуль и единицу иногда выносят в сигнатуру как нульместные операции.

Определяя алгебру, следует помнить, что результат применения любой операции должен принадлежать тому же множеству, что и её аргументы. Поэтому, в частности, 3-мерное пространство с векторным произведением является алгеброй, а со скалярным – нет.

Обобщение алгебры – многоосновные алгебры: увеличение числа носителей (основ): М={M₁, M₂,…, M_n}, при этом операции задаются на декартовых произведениях основ со значениями в каком-либо множестве M_k.

Иногда вместе с операциями на том же множестве рассматривают отношения (в действительности всегда есть отношение равенства элементов!) – в таких случаях можно использовать термин алгебраические системы (структуры, модели).