В этом методе кривая 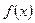 заменяется прямой линией – хордой, стягивающей точки
заменяется прямой линией – хордой, стягивающей точки 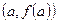 и
и 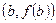 . В зависимости от знака выражения
. В зависимости от знака выражения 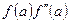 метод хорд имеет два варианта, изображенных на рис. 1.6, а, б.
метод хорд имеет два варианта, изображенных на рис. 1.6, а, б.
Пусть 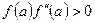 (рис. 1.6, а). Тогда
(рис. 1.6, а). Тогда 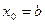 , точка
, точка 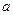 будет оставаться неподвижной. Следующее приближение
будет оставаться неподвижной. Следующее приближение 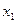 находим как точку пересечения хорды, соединяющей точки
находим как точку пересечения хорды, соединяющей точки 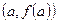 и
и 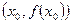 с осью
с осью 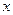 . Поскольку уравнение хорды записывается как
. Поскольку уравнение хорды записывается как 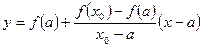 , то точка пересечения хорды с осью
, то точка пересечения хорды с осью 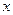 находится из выражения:
находится из выражения: 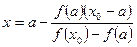 .
.
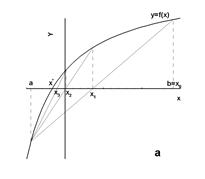 | 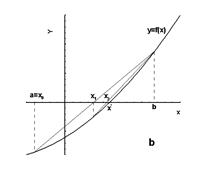 |
Рис. 1.6. Метод хорд для 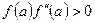 (a)и (a)и 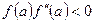 (b) (b) |
Пусть теперь 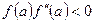 (рис. 1.6, б). Тогда
(рис. 1.6, б). Тогда 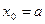 , точка
, точка 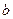 неподвижна. Проведем хорду, соединяющую точки
неподвижна. Проведем хорду, соединяющую точки 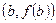 и
и 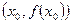 :
: 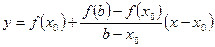 . Вычисляем точку пересечения хорды с осью
. Вычисляем точку пересечения хорды с осью 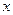 :
: 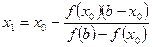 . На следующей итерации в качестве
. На следующей итерации в качестве 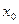 надо взять вычисленное значение
надо взять вычисленное значение 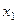 и т.д. Таким образом, мы получим следующую последовательность вычислений в зависимости от вида функции:
и т.д. Таким образом, мы получим следующую последовательность вычислений в зависимости от вида функции:
Если 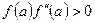 , то
, то 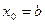 и
и 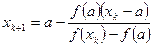 . Если же
. Если же 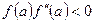 , то
, то 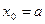 и
и 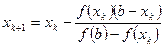 , где
, где 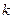 - номер итерации.
- номер итерации.
Окончание итерационного цикла в данном методе происходит либо по условию малости невязки уравнения: 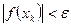 , либо по условию
, либо по условию 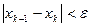 .
.
ПРИМЕР 1.5. Найти первый и третий корень уравнения 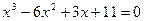 методом хорд.
методом хорд.
|
|
|
Концы интервала изоляции для первого корня 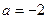 и
и 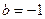 , соответственно. Проверим знак выражения
, соответственно. Проверим знак выражения 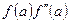 для данного уравнения:
для данного уравнения:
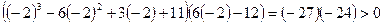 . Таким образом, расчет ведется по формулам:
. Таким образом, расчет ведется по формулам: 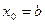 и
и 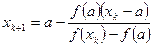 . В результате получим таблицу:
. В результате получим таблицу:
| Номер итерации | 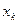 | 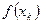 | 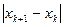 |
| -1 | - | ||
| -1.03571 | 0.345618 | 0.035714 | |
| -1.0479 | 0.117007 | 0.012187 | |
| -1.05201 | 0.039334 | 0.004108 | |
| -1.05339 | 0.013192 | 0.001379 | |
| -1.05385 | 0.004421 | 0.000462 |
Заданная точность достигнута на пятой итерации.
Для третьего корня 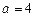 ,
, 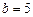 , и
, и 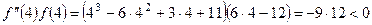 , следовательно, расчет ведется по вторым формулам:
, следовательно, расчет ведется по вторым формулам: 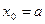 и
и 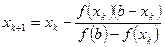 . Результаты вычислений показаны ниже:
. Результаты вычислений показаны ниже:
| Номер итерации | 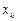 | 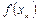 | 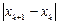 |
| -9 | - | ||
| 4.9 | -0.711 | 0.9 | |
| 4.941555 | -0.02147 | 0.041555 | |
| 4.942783 | -0.00062 | 0.001229 | |
| 4.942819 | -1.8E-05 | 3.57E-05 |
Заданная точность достигнута на четвертой итерации.
 2015-07-21
2015-07-21 1274
1274
