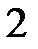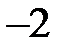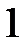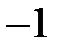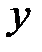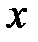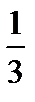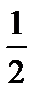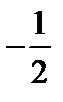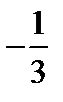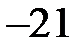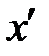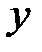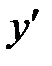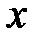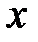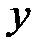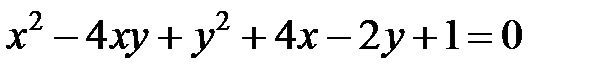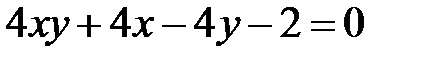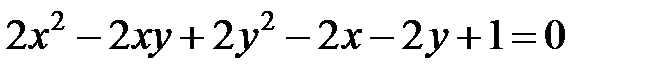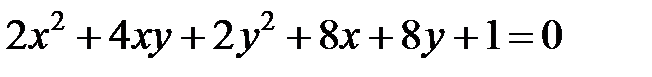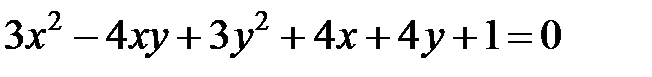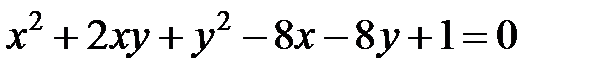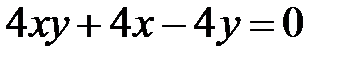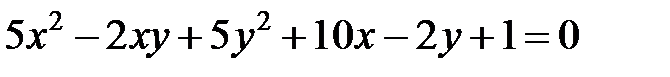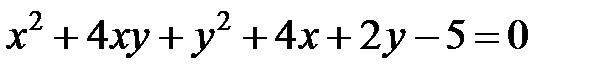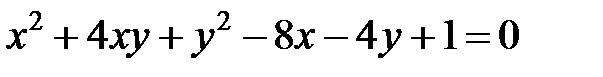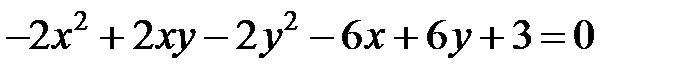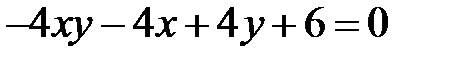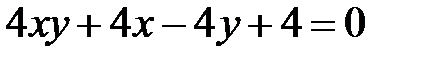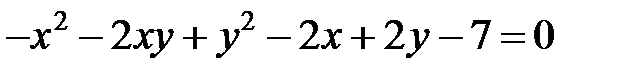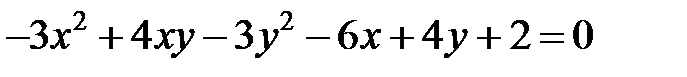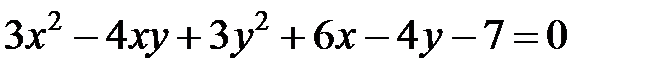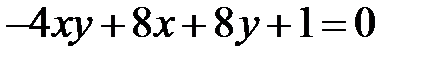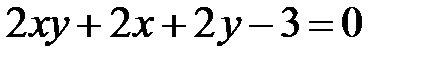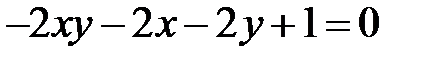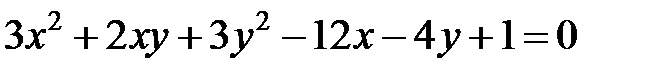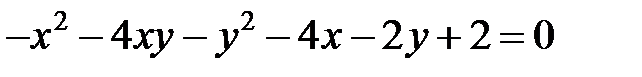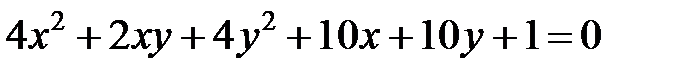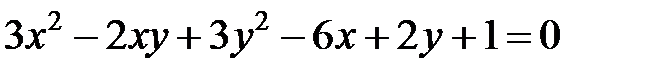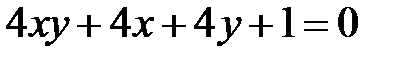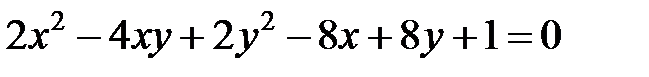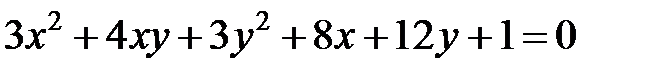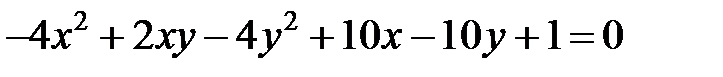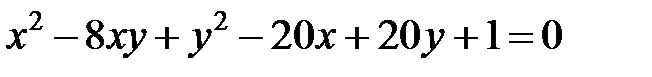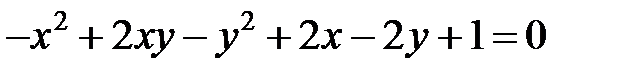Теперь рассмотрим уравнение кривой второго порядка, в котором коэффициент 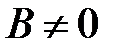 .
.
В этом случае необходимо применить преобразование поворота осей координат по формулам:
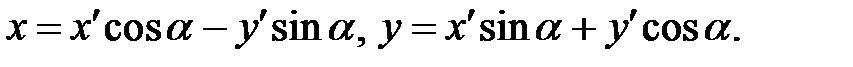 | (13) |
При этом угол 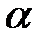 подбирается таким образом, чтобы уравнение стало пятичленным, т.е. не содержащим произведения
подбирается таким образом, чтобы уравнение стало пятичленным, т.е. не содержащим произведения 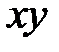 . Дальнейшие преобразования аналогичны приведенным выше преобразованиям для пятичленного уравнения.
. Дальнейшие преобразования аналогичны приведенным выше преобразованиям для пятичленного уравнения.
3. Примеры выполнения заданий типового расчета
Задача 1. Составить каноническое уравнение эллипса и гиперболы с полуосями 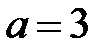 и
и 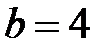 , выписать координаты фокусов.
, выписать координаты фокусов.
Решение.
Составим сначала уравнение эллипса по формуле (2):
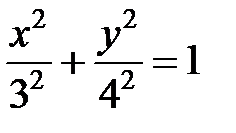 или
или 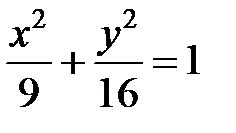 .
.
Так как 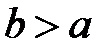 , то фокусы имеют координаты
, то фокусы имеют координаты 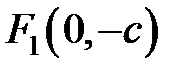 и
и 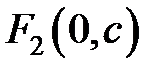 , где
, где 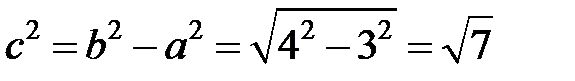 . Т.е. координаты фокусов
. Т.е. координаты фокусов 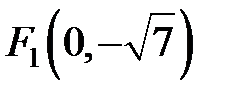 и
и 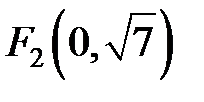 .
.
Составим уравнение гиперболы, для которой действительная полуось 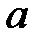 , а мнимая –
, а мнимая – 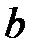 . Воспользуемся формулой (5). Получим
. Воспользуемся формулой (5). Получим
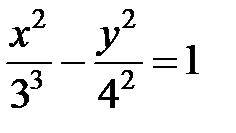 или
или 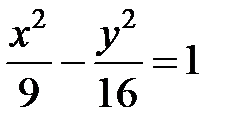 .
.
Для гиперболы 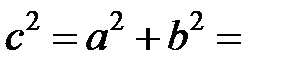
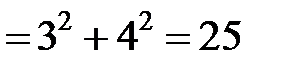 . Поэтому фокусы имеют координаты
. Поэтому фокусы имеют координаты 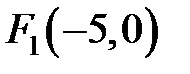 и
и 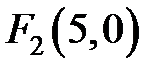 .
.
В случае, когда полуось 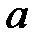 является мнимой, а полуось
является мнимой, а полуось 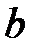 – действительной, получим по формуле (6)
– действительной, получим по формуле (6)
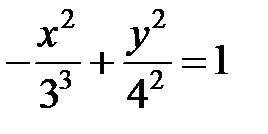 или
или 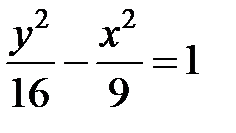 .
.
Фокусы данной параболы имеют координаты 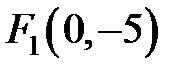 и
и 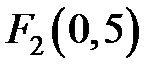 .
.
Задача 2. Составить канонические уравнения парабол с параметром 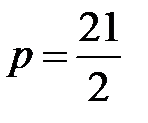 , выписать координаты фокуса и уравнение директрисы.
, выписать координаты фокуса и уравнение директрисы.
Решение.
В случае, когда парабола симметрична относительно оси 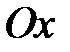 , ее уравнение, согласно формуле (9), имеет вид
, ее уравнение, согласно формуле (9), имеет вид 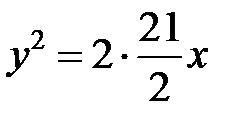 или
или 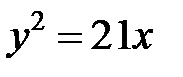 . При этом фокус лежит на оси
. При этом фокус лежит на оси 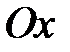 на расстоянии
на расстоянии 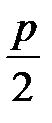 от начала координат, т.е. координаты фокуса
от начала координат, т.е. координаты фокуса 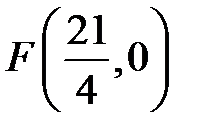 , уравнение директрисы имеет вид
, уравнение директрисы имеет вид 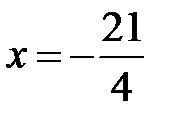 .
.
Если же осью симметрии параболы является ось 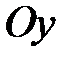 , то уравнение примет вид
, то уравнение примет вид 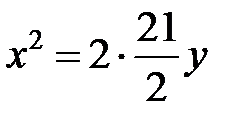 или
или 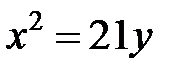 . Соответственно, фокус находится на оси
. Соответственно, фокус находится на оси 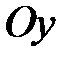 , имеет координаты
, имеет координаты 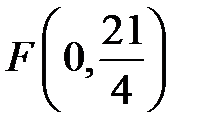 , а уравнение директрисы:
, а уравнение директрисы: 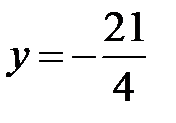 .
.
Задача 3. Построить кривые 2-го порядка, заданные уравнениями:
а) 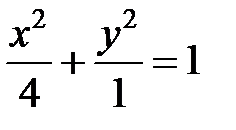 ; б)
; б) 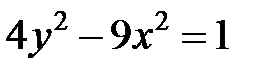 ; в)
; в) 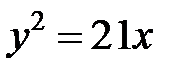 .
.
Решение.
а) Данное уравнение задает эллипс с полуосями 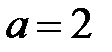 и и 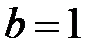 . Для построения отложим от начала координат в обе стороны расстояние . Для построения отложим от начала координат в обе стороны расстояние 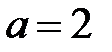 на оси на оси 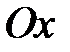 и и 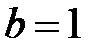 на оси на оси 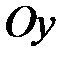 . Используя полученные точки, построим прямоугольник со сторонами . Используя полученные точки, построим прямоугольник со сторонами 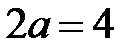 и и 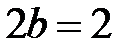 , а в прямоугольник впишем эллипс (рис. 7). , а в прямоугольник впишем эллипс (рис. 7). |
Рис. 7 |
б) Уравнение преобразуем к виду 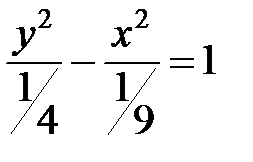 или
или 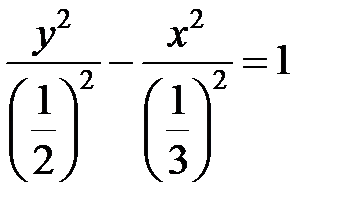 . Значит, это гипербола, симметричная относительно оси
. Значит, это гипербола, симметричная относительно оси 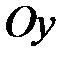 , с действительной ось
, с действительной ось 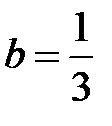 и мнимой осью
и мнимой осью 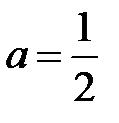 . Для построения отложим от начала координат в обе стороны
. Для построения отложим от начала координат в обе стороны 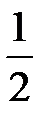 по оси
по оси 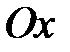 и
и 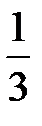 по оси
по оси 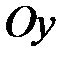 (рис. 8). Аналогично случаю а) построим прямоугольник, затем проведем в нем диагонали и продлим их за прямоугольник.
(рис. 8). Аналогично случаю а) построим прямоугольник, затем проведем в нем диагонали и продлим их за прямоугольник.
Данные диагонали являются асимптотами гиперболы. Ветви гиперболы будут располагаться выше и ниже построенного прямоугольника, их вершинами являются точки 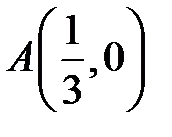 и и 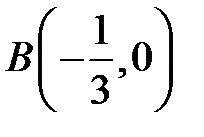 . По мере удаления от начала координат ветви гиперболы будут неограниченно приближаться к асимптотам, но никогда их не пересекут. . По мере удаления от начала координат ветви гиперболы будут неограниченно приближаться к асимптотам, но никогда их не пересекут. |
Рис.8 | ||||||
в) Уравнение задает параболу, симметричную относительно оси 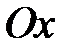 и направленную влево. Вершиной параболы является начало координат. Для построения найдем пару дополнительных точек. Ими являются, например, и направленную влево. Вершиной параболы является начало координат. Для построения найдем пару дополнительных точек. Ими являются, например, 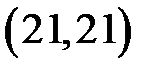 и и 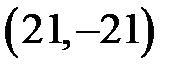 . Можно найти еще несколько точек, вычислив их координаты хотя бы приблизительно. . Можно найти еще несколько точек, вычислив их координаты хотя бы приблизительно. |
Рис 9 |
Задача 3. Привести к каноническому виду уравнение 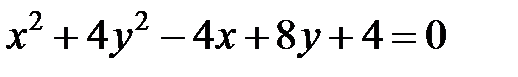 . Найти координаты фокусов. Построить кривую.
. Найти координаты фокусов. Построить кривую.
Решение.
Сгруппируем слагаемые и дополним до полного квадрата. Получим:
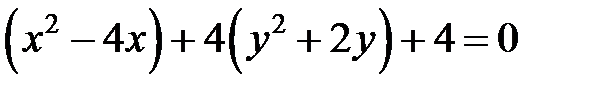 ,
, 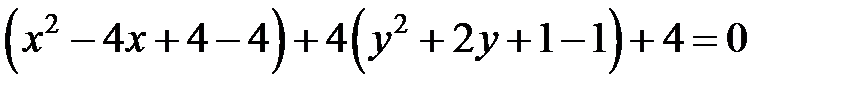 ,
, 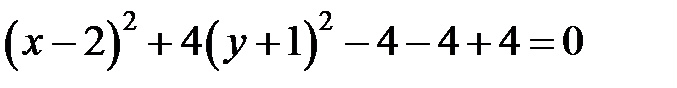 ,
, 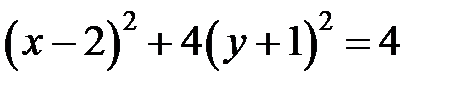 ,
, 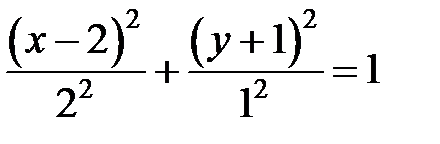 .
.
Перенесем начало координат в точку 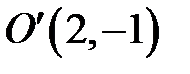 (рис. 10) и применим преобразование координат
(рис. 10) и применим преобразование координат 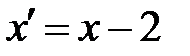 ,
, 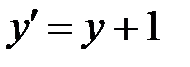 , получим уравнение эллипса:
, получим уравнение эллипса:
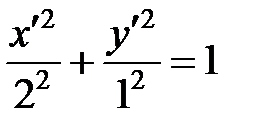 .
.
Полуоси данного эллипса 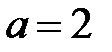 , , 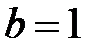 . Так как . Так как 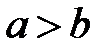 , то , то 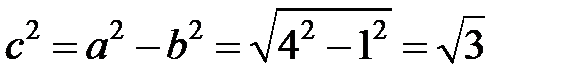 . Координаты фокусов в новой системе координат . Координаты фокусов в новой системе координат 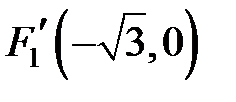 и и 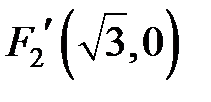 . Из преобразования координат имеем: . Из преобразования координат имеем: 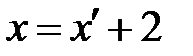 , , 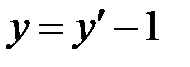 , поэтому фокусы в исходной системе координат выглядят так: , поэтому фокусы в исходной системе координат выглядят так: 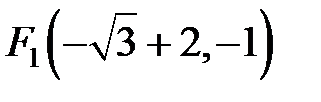 и и 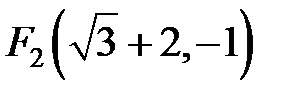 . . |
|
Задача 4. Привести уравнение 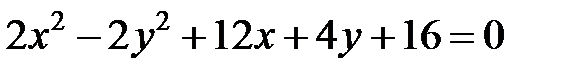 к каноническому виду, сделать чертеж, если это возможно.
к каноническому виду, сделать чертеж, если это возможно.
Решение.
Сгруппируем слагаемые, сразу дополняя до полного квадрата:
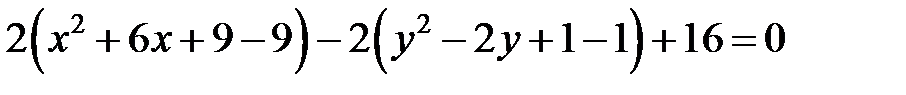
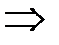
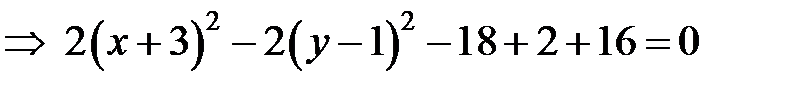
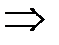
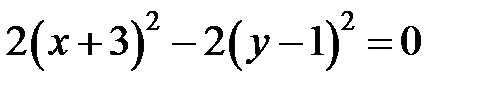 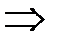 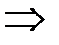 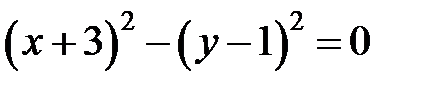  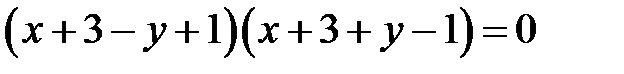   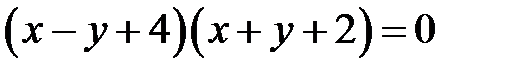 . Т.е. данная кривая распадается на пару пересекающихся прямых, задаваемых уравнениями . Т.е. данная кривая распадается на пару пересекающихся прямых, задаваемых уравнениями 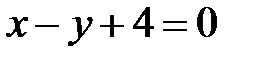 и и 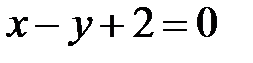 (рис. 11). (рис. 11). |
Рис. 11 |
Задача 5. Составить уравнение кривой, для каждой точки которой расстояние до точки 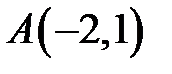 в 2 раза больше расстояния до прямой
в 2 раза больше расстояния до прямой 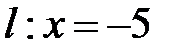 .
.
Решение.
Пусть 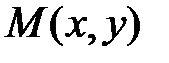 – произвольная точка искомой кривой. Тогда расстояние
– произвольная точка искомой кривой. Тогда расстояние 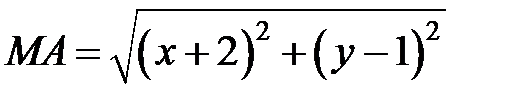 . Так как прямая
. Так как прямая 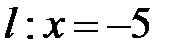 перпендикулярна оси
перпендикулярна оси 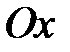 , то расстояние до нее от точки
, то расстояние до нее от точки 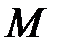 равно
равно 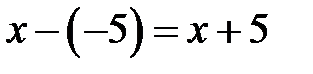 . Тогда по условию получаем:
. Тогда по условию получаем:
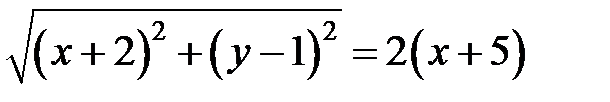 .
.
Возведем обе части полученного равенства в квадрат и проведем необходимые преобразования:
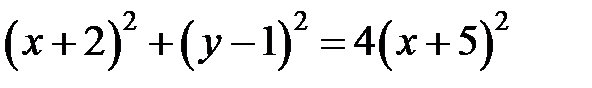
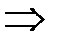
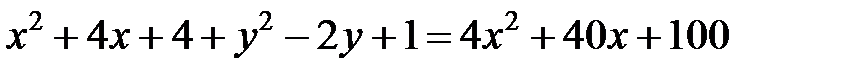
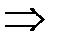
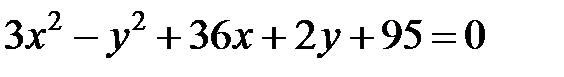
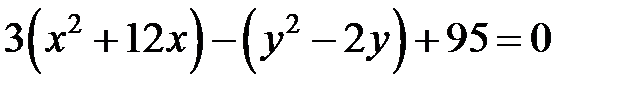
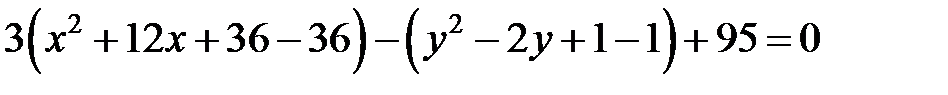
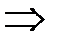
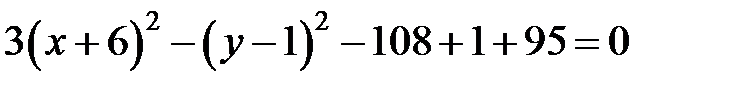
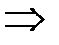
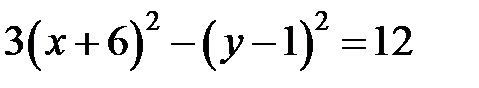
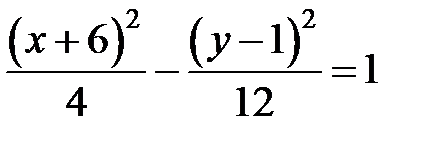 .
.
Применив преобразование координат 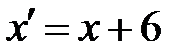 ,
, 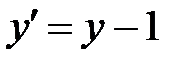 , получим каноническое уравнение гиперболы
, получим каноническое уравнение гиперболы 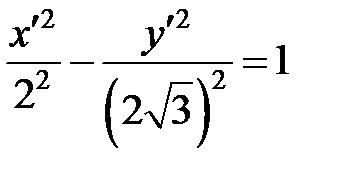 . Т.е искомая кривая – это гипербола с центром симметрии
. Т.е искомая кривая – это гипербола с центром симметрии 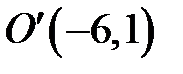 .
.
Задача 6. Привести уравнение 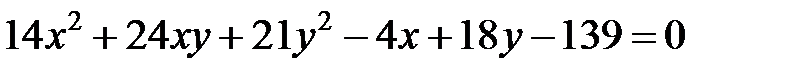 к каноническому виду. Определить тип кривой.
к каноническому виду. Определить тип кривой.
Решение.
Применим преобразования (13), получим:
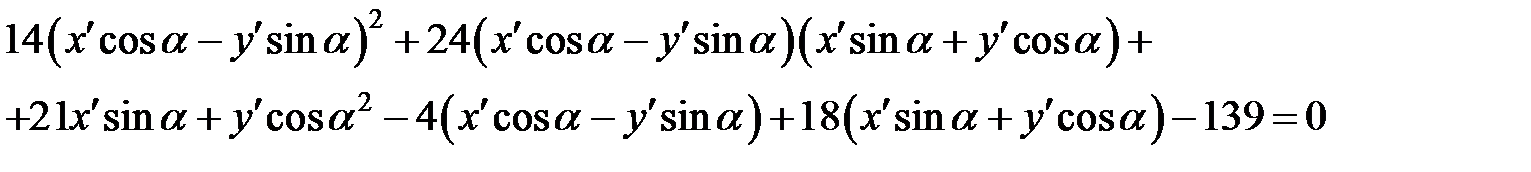
Раскроем скобки и приведем подобные:
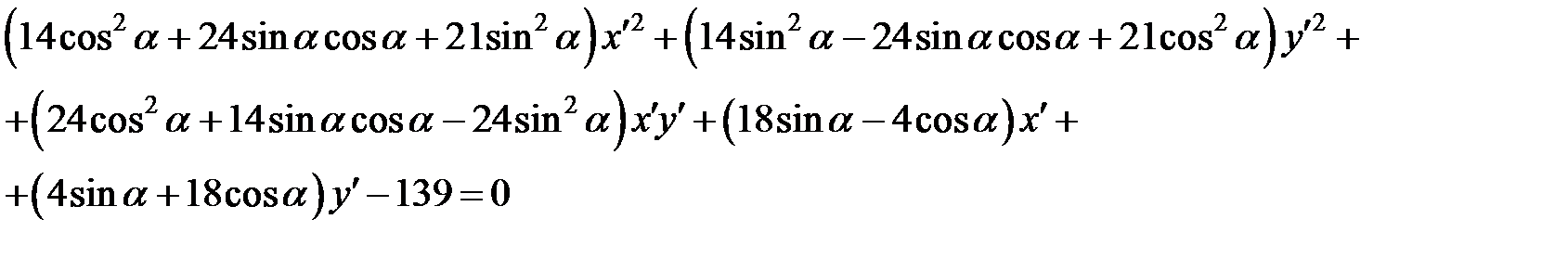
Приравняем к нулю коэффициент при 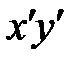 и, решив тригонометрическое уравнение, найдем
и, решив тригонометрическое уравнение, найдем 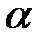 .
.
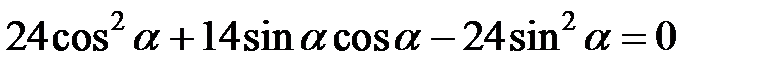 или
или 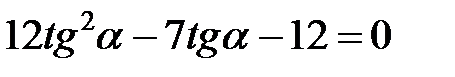 ,
,
откуда 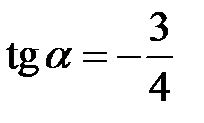 или
или 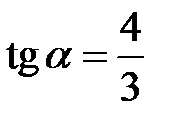 . Очевидно, что эти значения тангенса соответствуют двум перпендикулярным направлениям, поэтому достаточно взять одно из них, т.к. при втором мы просто поменяем местами
. Очевидно, что эти значения тангенса соответствуют двум перпендикулярным направлениям, поэтому достаточно взять одно из них, т.к. при втором мы просто поменяем местами 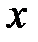 и
и 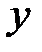 . Возьмем
. Возьмем 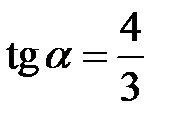 . Тогда
. Тогда 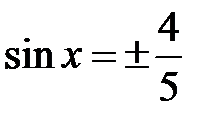 ,
, 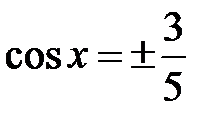 . Пусть
. Пусть 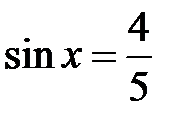 ,
, 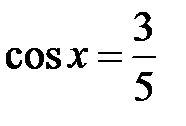 . Т.е. совершаем поворот координатных осей на угол
. Т.е. совершаем поворот координатных осей на угол 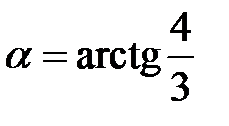 . Подставим в уравнение и получим:
. Подставим в уравнение и получим:
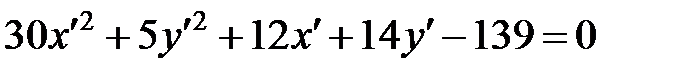 .
.
Теперь выделяем полные квадраты, аналогично случаю пятичленного уравнения.
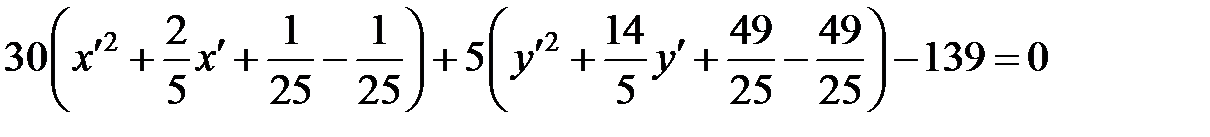 ,
,
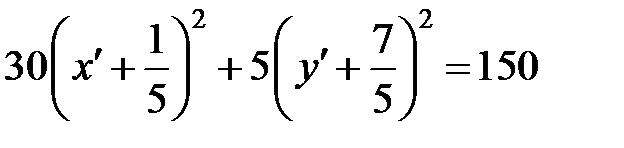 ,
, 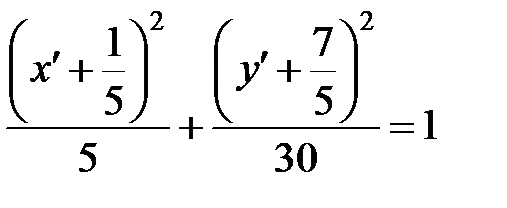 .
.
Возьмем за новое начало координат точку 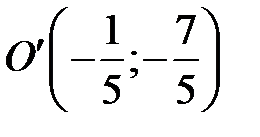 и, применив преобразование координат
и, применив преобразование координат 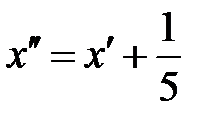 ,
, 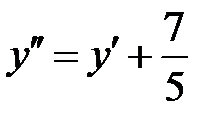 , получим уравнение эллипса:
, получим уравнение эллипса:
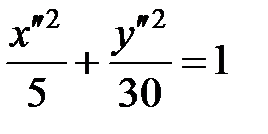 .
.
Полуоси данного эллипса: 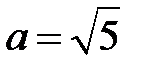 и
и 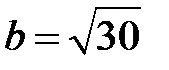 .
.
4. Варианты типового расчета «Кривые второго порядка»
Задание 1.
а) Составить каноническое уравнение эллипса (в нечетных вариантах) или гиперболы (в четных вариантах) с полуосями 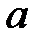 и
и 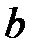 (в вариантах 2, 6, 10, 14, 18, 22, 26 и 30 действительная полуось
(в вариантах 2, 6, 10, 14, 18, 22, 26 и 30 действительная полуось 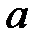 , мнимая –
, мнимая – 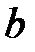 , в вариантах 4, 8, 12, 16, 20, 24, 28 – наоборот) по данным табл. 1., выписать координаты фокусов.
, в вариантах 4, 8, 12, 16, 20, 24, 28 – наоборот) по данным табл. 1., выписать координаты фокусов.
б) Составить каноническое уравнение параболы с заданными параметром 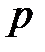 и осью симметрии по данным табл. 1, выписать координаты фокуса и уравнение директрисы.
и осью симметрии по данным табл. 1, выписать координаты фокуса и уравнение директрисы.
Таблица 1
| Вариант | Данные | Вариант | Данные | ||||||
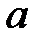 | 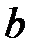 | 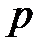 | Ось симметрии | 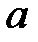 | 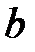 | 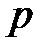 | Ось симметрии | ||
| 5,5 | Ox | –0,75 | Ox | ||||||
| 3,5 | Oy | 6,5 | Ox | ||||||
| –5 | Oy | Oy | |||||||
| –4,5 | Ox | –4,75 | Oy | ||||||
| Ox | –8,5 | Ox | |||||||
| 2,5 | Oy | Ox | |||||||
| –3 | Oy | 0,25 | Oy | ||||||
| –0,5 | Ox | –1,25 | Oy | ||||||
| Ox | –9 | Ox | |||||||
| 1,5 | Oy | 9,5 | Ox | ||||||
| –1 | Oy | 2,75 | Oy | ||||||
| –3,25 | Ox | –1,75 | Oy | ||||||
| Ox | –4,75 | Ox | |||||||
| 3,75 | Oy | 7,5 | Ox | ||||||
| –7 | Oy | 4,25 | Oy |
Задание 2. Выбрав соответствующий масштаб, построить кривые 2-го порядка, заданные уравнениями, приведенными в табл. 2.
Таблица 2
| Вариант | Уравнения кривых | ||
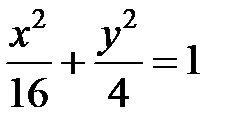 ; ; | 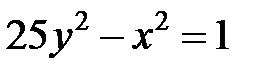 ; ; | 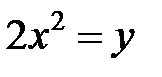 | |
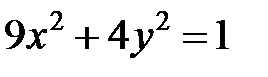 ; ; | 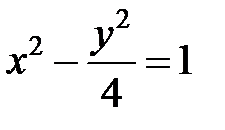 ; ; | 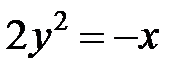 | |
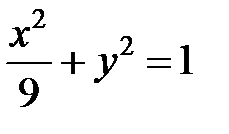 ; ; | 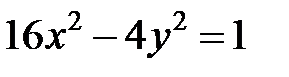 ; ; | 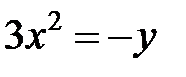 | |
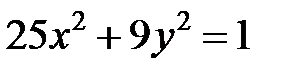 ; ; | 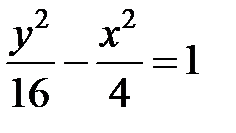 ; ; | 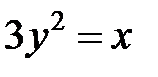 | |
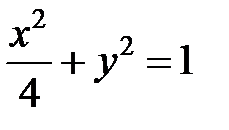 ; ; | 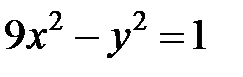 ; ; | 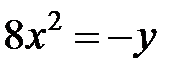 | |
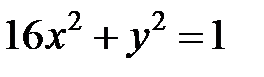 ; ; | 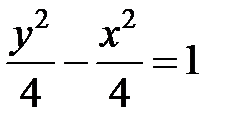 ; ; | 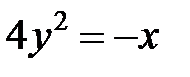 | |
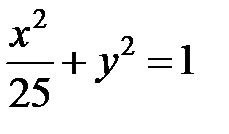 ; ; | 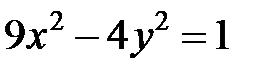 ; ; | 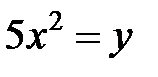 | |
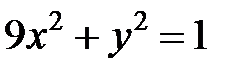 ; ; | 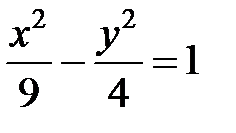 ; ; | 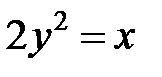 | |
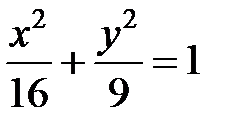 ; ; | 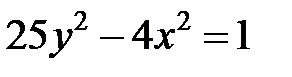 ; ; | 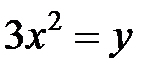 | |
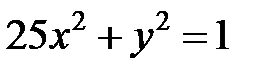 ; ; | 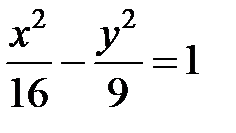 ; ; | 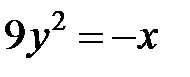 | |
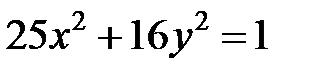 ; ; | 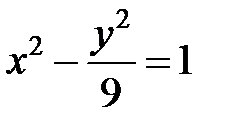 ; ; | 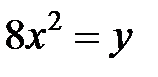 | |
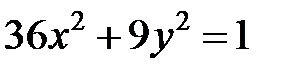 ; ; | 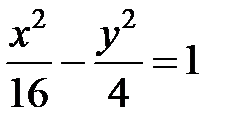 ; ; | 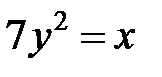 | |
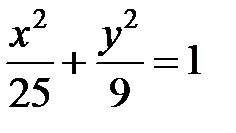 ; ; | 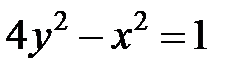 ; ; | 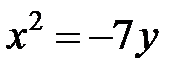 | |
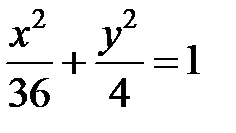 ; ; | 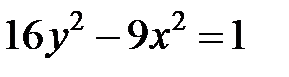 ; ; | 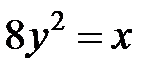 | |
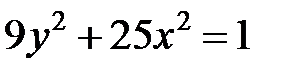 ; ; | 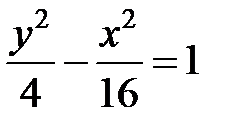 ; ; | 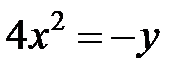 | |
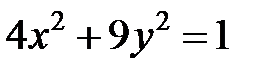 ; ; | 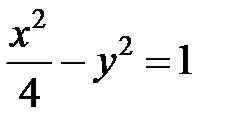 ; ; | 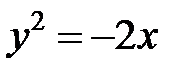 |
Таблица 2 (окончание)
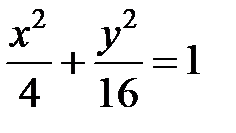 ; ; | 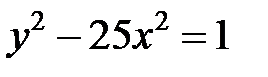 ; ; | 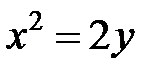 | |
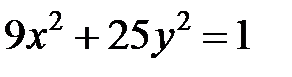 ; ; | 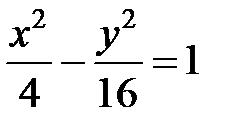 ; ; | 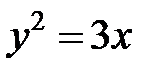 | |
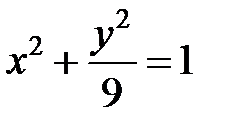 ; ; | 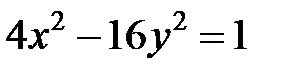 ; ; | 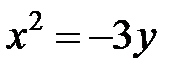 | |
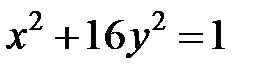 ; ; | 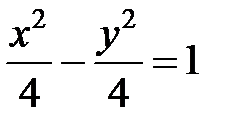 ; ; | 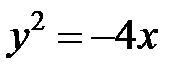 | |
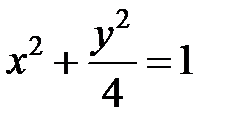 ; ; | 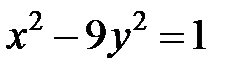 ; ; | 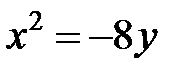 | |
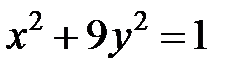 ; ; | 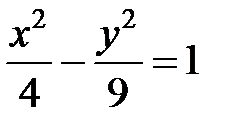 ; ; | 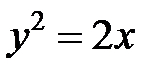 | |
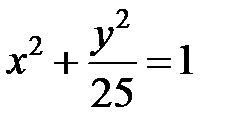 ; ; | 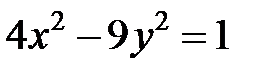 ; ; | 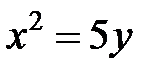 | |
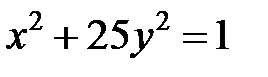 ; ; | 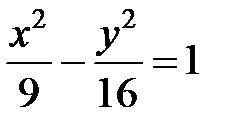 ; ; | 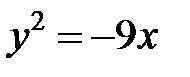 | |
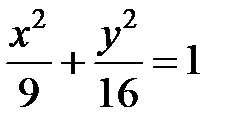 ; ; | 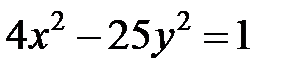 ; ; | 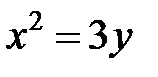 | |
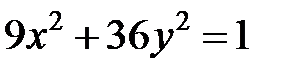 ; ; | 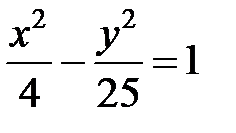 ; ; | 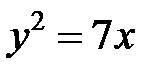 | |
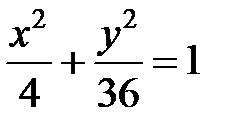 ; ; | 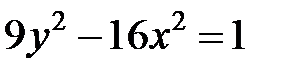 ; ; | 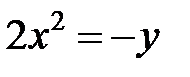 | |
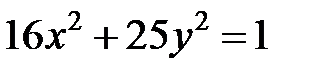 ; ; | 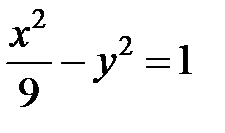 ; ; | 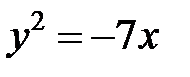 | |
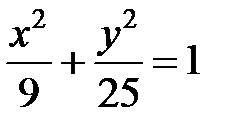 ; ; | 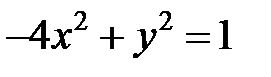 ; ; | 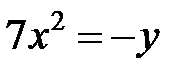 | |
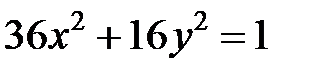 ; ; | 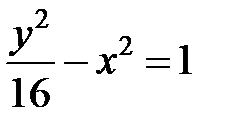 ; ; | 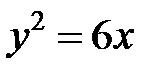 |
Задание 3. Привести уравнения кривых второго порядка к каноническому виду (табл. 3), построить кривые, найти координаты фокусов.
Таблица 3
| Вариант | Уравнение кривой | |
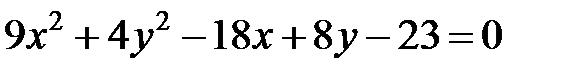 ; ; | 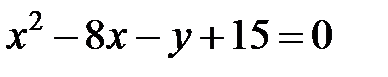 | |
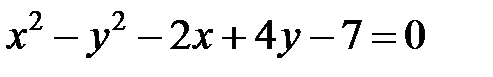 ; ; | 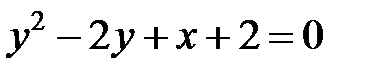 | |
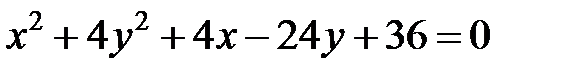 ; ; | 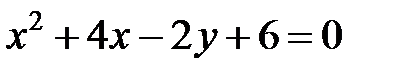 | |
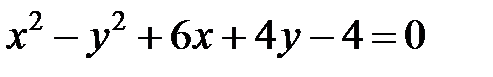 ; ; | 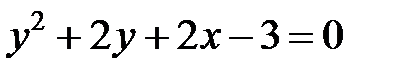 | |
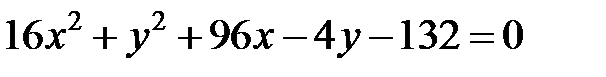 ; ; | 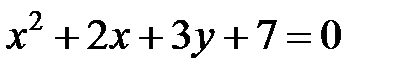 | |
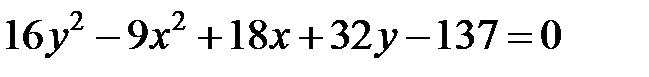 ; ; | 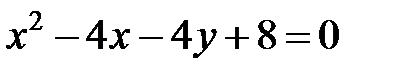 | |
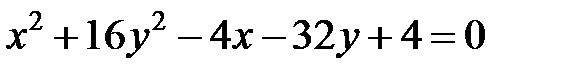 ; ; | 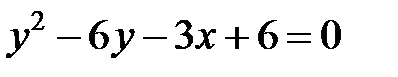 | |
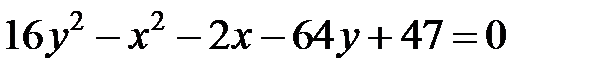 ; ; | 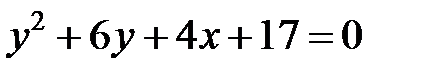 | |
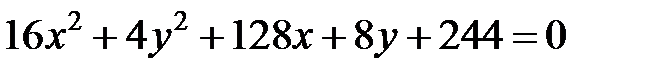 ; ; | 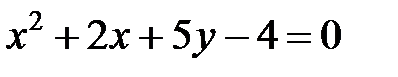 | |
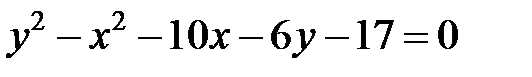 ; ; | 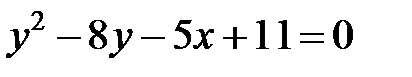 | |
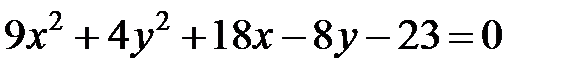 ; ; | 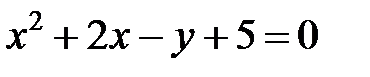 | |
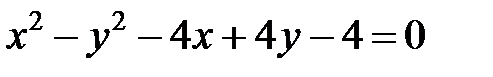 ; ; | 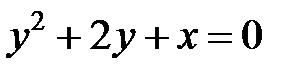 | |
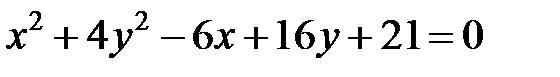 ; ; | 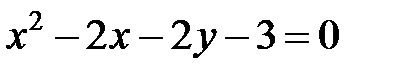 | |
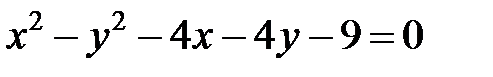 ; ; | 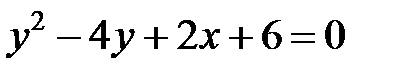 | |
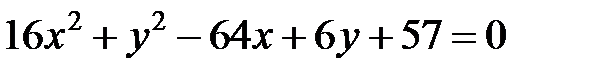 ; ; | 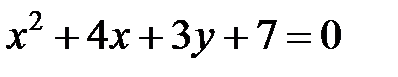 | |
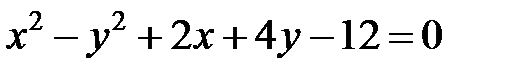 ; ; | 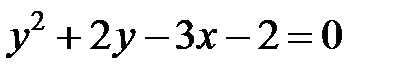 | |
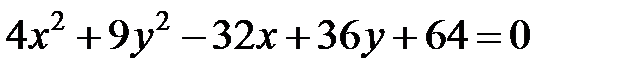 ; ; | 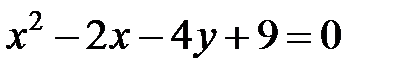 | |
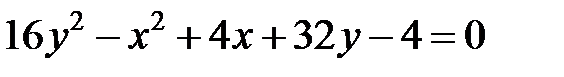 ; ; | 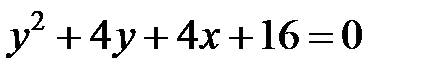 | |
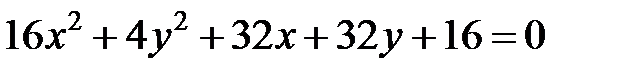 ; ; | 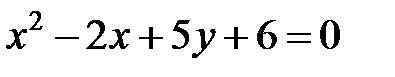 | |
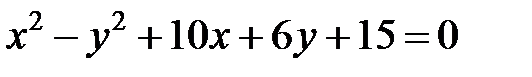 ; ; | 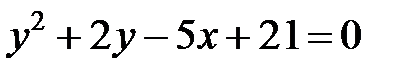 | |
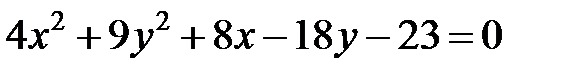 ; ; | 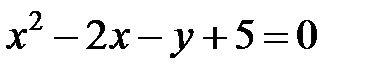 | |
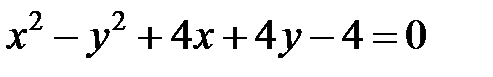 ; ; | 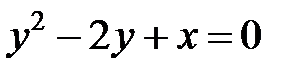 | |
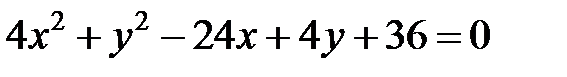 ; ; | 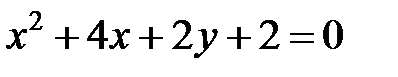 | |
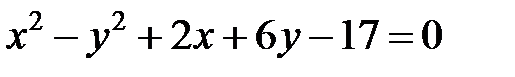 ; ; | 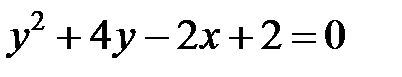 | |
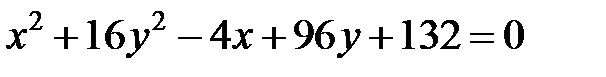 ; ; | 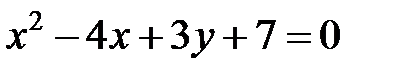 | |
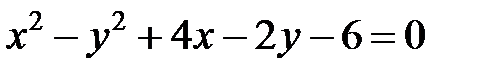 ; ; | 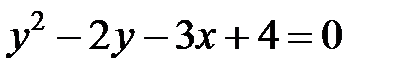 |
Таблица 3 (окончание)
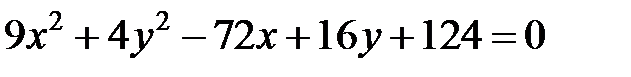 ; ; | 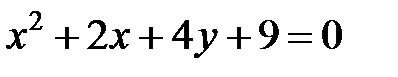 | |
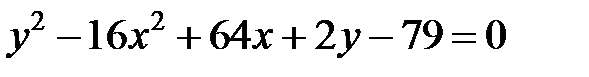 ; ; | 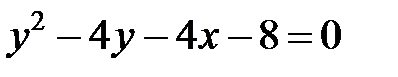 | |
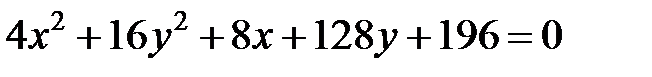 ; ; | 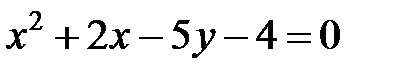 | |
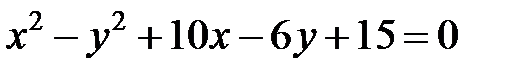 ; ; | 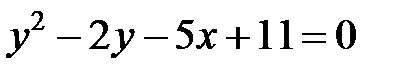 |
Задание 4. Привести уравнение кривой второго порядка к каноническому виду (табл. 4), сделать чертеж, если это возможно.
Таблица 4
| Вари-ант | Уравнение кривой | Вари-ант | Уравнение кривой |
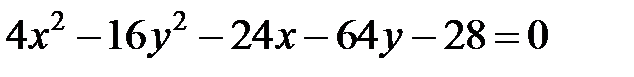 | 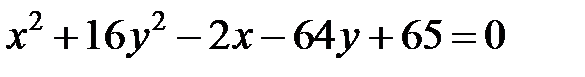 | ||
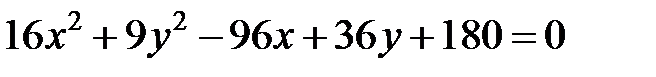 | 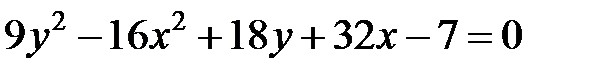 | ||
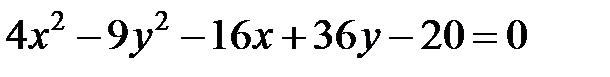 | 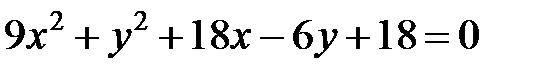 | ||
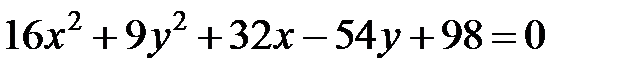 | 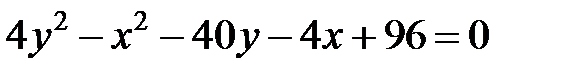 | ||
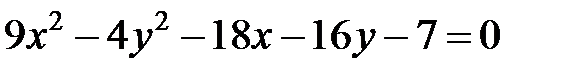 | 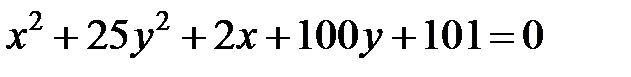 | ||
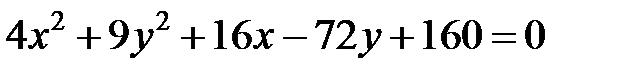 | 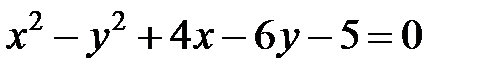 | ||
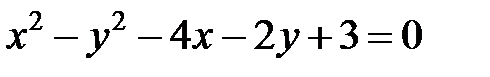 | 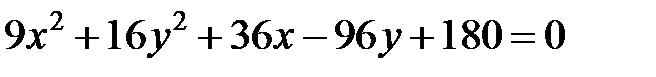 | ||
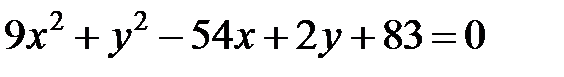 | 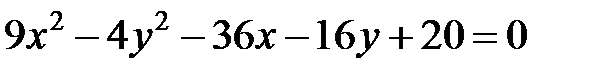 | ||
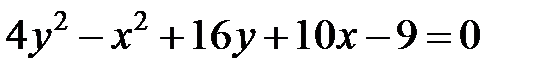 | 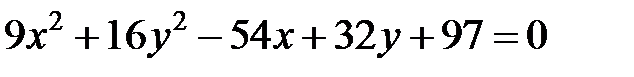 | ||
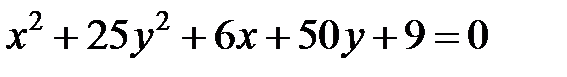 | 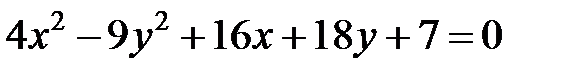 | ||
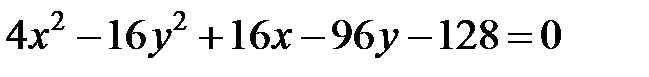 | 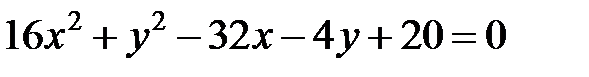 | ||
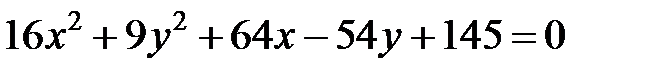 | 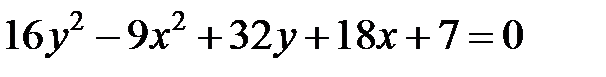 | ||
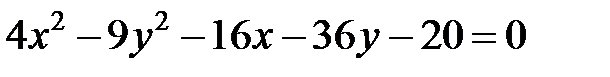 | 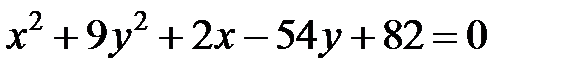 | ||
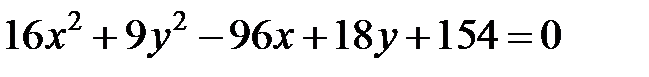 | 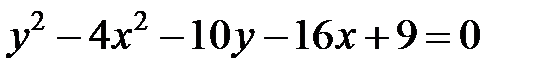 | ||
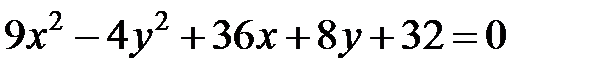 | 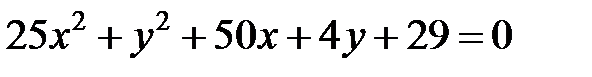 |
Задание 5. Найти уравнение кривой на плоскости, используя заданные геометрические свойства кривой (табл. 5), привести полученное уравнение к каноническому виду, указать тип кривой. Для каждой точки кривой отношение расстояния до точки 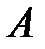 к расстоянию до прямой
к расстоянию до прямой  равно
равно 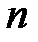 .
.
Таблица 5
| Вари-ант | Исходные данные | Вари-ант | Исходные данные | ||||
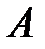 | 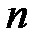 |  | 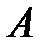 | 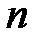 |  | ||
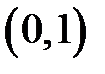 | 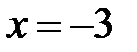 | 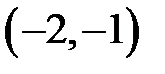 | 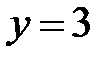 | ||||
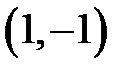 | 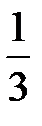 | 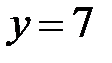 | 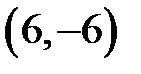 | 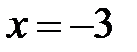 | |||
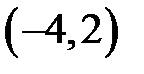 | 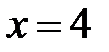 | 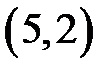 | 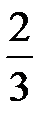 | 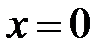 | |||
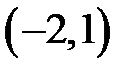 | 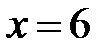 | 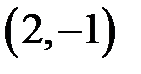 |  | ||||
 |  |  | 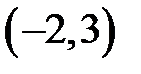 | 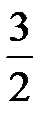 | 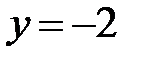 | ||
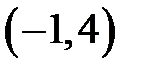 | 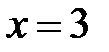 | 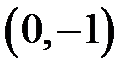 | 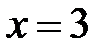 | ||||
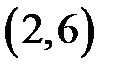 |  |  |  |  | |||
 |  |  |  |  | |||
 |  |  |  | ||||
 |  |  | 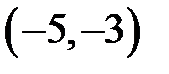 | 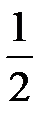 | 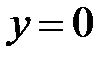 | ||
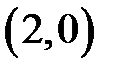 | 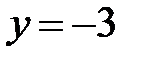 | 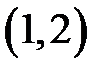 | 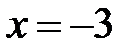 | ||||
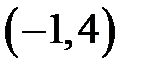 | 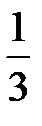 | 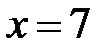 | 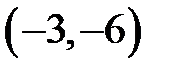 | 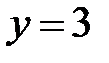 | |||
 |  |  |  | 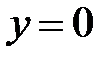 | |||
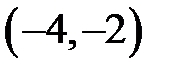 | 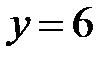 | 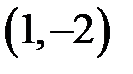 | 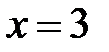 | ||||
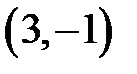 | 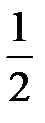 | 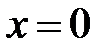 | 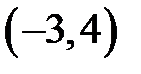 | 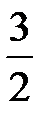 | 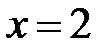 |
Задание 6. Исследовать кривую второго порядка и привести ее уравнение к каноническому виду (табл. 6).
Таблица 6
 2015-07-14
2015-07-14 3111
3111