Выпуклость вверх и вниз

Функция f(x) имеет выпуклость вверх (вниз) в точке x 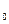, если касательная в окрестности этой точки располагается выше (ниже) этой кривой.

Задача 1

Пусть функция f(x) непрерывна и имеет производные первого и второго порядка.

Показать, что по знаку производной второго порядка можно судить о том, функция в этой точке выпукла вверх или вниз.

Ø Формулу Тейлора

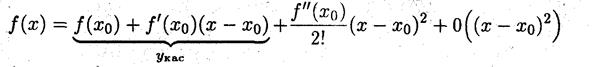
можно записать в следующем виде:

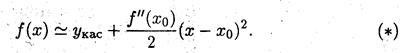
По определению, если f(x) <yкас то функция выпукла вверх, а если f(x)>yкас, то функция выпукла вниз. Таким образом из формулы (*) следует:

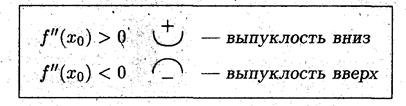
Точка x 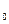называется точкой перегиба, если она разделя­ет у непрерывной функции области выпуклости вверх и вниз.

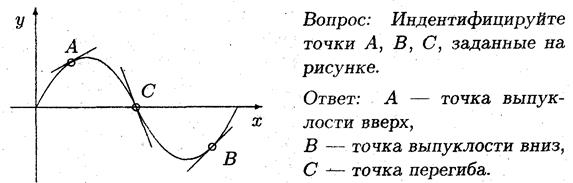
• Проходящая через точку перегиба касательная, частично ле­жит выше кривой, а частично ниже.

Необходимые условия точки перегиба: