На рисунке 1.4 изображено осевое сечение цилиндрической стенки.
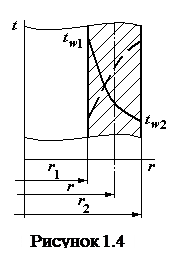 Пусть на границах цилиндрической стенки заданы граничные условия первого рода:
Пусть на границах цилиндрической стенки заданы граничные условия первого рода:
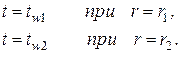 (1.14)
(1.14)
При длине стенки 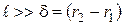 тепловой поток имеет радиальное направление, а температурное поле одномерное, то есть
тепловой поток имеет радиальное направление, а температурное поле одномерное, то есть 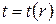 .
.
Для стационарной одномерной задачи о теплопроводности цилиндрической стенки без внутренних источников теплоты дифференциальное уравнение (1.5) в цилиндрической системе координат при постоянном коэффициенте теплопроводности (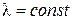 ) можно привести к виду:
) можно привести к виду:
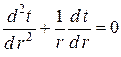 . (1.15)
. (1.15)
Введя новую переменную 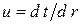 , преобразуем уравнение (1.15):
, преобразуем уравнение (1.15):
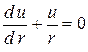 .
.
После разделения переменных и интегрирования полученного уравнения получим:
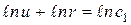 . (1.16)
. (1.16)
Потенциируя уравнение (1.16), найдём 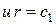 . Возвращаясь к перевоначальным переменным, запишем:
. Возвращаясь к перевоначальным переменным, запишем:
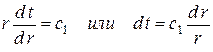 .
.
Интегрируя последнее уравнение, получим общее решение, описывающее распределение температуры в цилиндрической стенке:
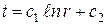 . (1.17)
. (1.17)
Искривление линии температуроно поля в цилиндрической стенке обусловлено изменением плотности теплового потока, равного 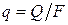 , при изменении радиуса цилиндра. При увеличении радиуса r величина площади
, при изменении радиуса цилиндра. При увеличении радиуса r величина площади 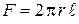 , где
, где 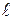 - длина стенки, также увеличивается. Поэтому при большей величине радиуса температурная линия проходит положе и, наоборот, при малых величинах радиуса – более круто. Это правило сохраняется также при обратном направлении теплового потока (см. пунктир на рисунке 1.4).
- длина стенки, также увеличивается. Поэтому при большей величине радиуса температурная линия проходит положе и, наоборот, при малых величинах радиуса – более круто. Это правило сохраняется также при обратном направлении теплового потока (см. пунктир на рисунке 1.4).
Определим две константы интегрирования, входящие в полученное общее решение (1.17). Для этого воспользуемя двумя граничными условиями первого рода (1.14). В результате найдём:
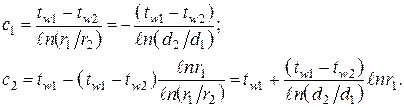 (1.18)
(1.18)
Преобразуем общее решение (1.17), подставив в него значения констант интегрирования (1.18):
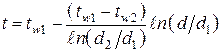 , (1.19)
, (1.19)
где 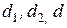 - внутренний, наружный и текущий диаметры цилиндрической стенки.
- внутренний, наружный и текущий диаметры цилиндрической стенки.
Используя формулу (1.19), определим градиент температуры в стенке:
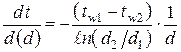 . (1.20)
. (1.20)
Найдём тепловой поток через стенку по формуле Фурье:
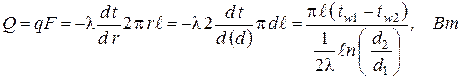 . (1.21)
. (1.21)
Поделив обе части формулы (1.21), определим тепловой поток, приходящийся на единицу длины цилиндрической стенки:
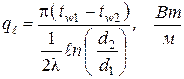 . (1.22)
. (1.22)
Величину 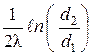 называют внутренним термическим сопротивлением цилиндрической стенки.
называют внутренним термическим сопротивлением цилиндрической стенки.
Обозначим плотность теплового потока на внутренней и внешней поверхности стенки соответственно параметрами 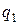 и
и 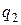 . Так как при стационарном режиме поток теплоты через цилиндрическую стенку одинаков, то можно записать соотношение:
. Так как при стационарном режиме поток теплоты через цилиндрическую стенку одинаков, то можно записать соотношение:
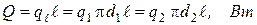 .
.
Из него найдём связь между параметрами 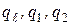 :
:
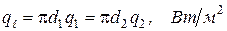 . (1.23)
. (1.23)
 2015-07-14
2015-07-14 780
780








