Смешанные стратегии

Если игра не имеет седловой точки, то применение чистых стратегий не даст оптимального решения игры. В этом случае применяют смешанные стратегии.

Определение. Смешанная стратегия игрока есть вероятностное распределение на множестве его чистых стратегий.

В случае, когда игрок А имеет p чистых стратегий 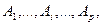смешанная стратегия представляет собой вектор 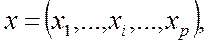удовлетворяющий условиям:

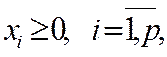(1.3)

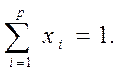(1.4)

Аналогично, вектором 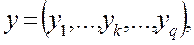удовлетворяющим условиям

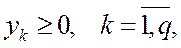(1.5)

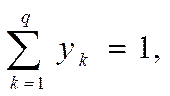(1.6)

определяется смешанная стратегия игрока В.

Числа 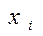и 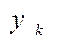можно интерпретировать как вероятности использования стратегий 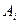первым игроком и 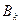- вторым игроком. Чистые стратегии являются частным случаем смешанной стратегии, задаваемой единичным вектором.

Функцией выигрыша, или платежной функцией 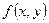игры с матрицей 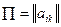при применении игроком А смешанной стратегии 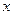, а игроком В – смешанной стратегии 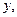называется математическое ожидание выигрыша игрока А (проигрыша В), подсчитываемое по формуле

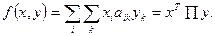(1.7)

Стратегии 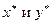называются оптимальными, если выполняются неравенства

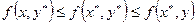(1.8)

для любых х из множества Х смешанных стратегий игрока А и любых 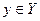- множества смешанных стратегий игрока В.

Таким образом, если игрок А применяет свою оптимальную смешанную стратегию 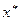, то ему всегда гарантирован средний выигрыш 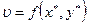, как бы при этом ни выбирал игрок В различные свои смешанные стратегии. Аналогично, применение игроком В своей оптимальной смешанной стратегии 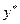обеспечивает ему проигрыш не более, чем 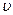при любых смешанных стратегиях противника.

Совокупность оптимальных стратегий 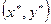называется оптимальным решением, или просто решением игры, а значение платежной функции при этом – ценой игры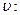

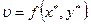(1.9)

Фундаментальная теорема фон Неймана утверждает, что каждая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.