Векторное произведение двух векторов

ОПРЕДЕЛЕНИЕ 4.2. ТРИ ВЕКТОРА НАЗОВЁМ НЕКОМПЛАНАРНЫМИ, ЕСЛИ ОНИ НЕ ЛЕЖАТ НИ В КАКОЙ ОДНОЙ И ТОЙ ЖЕ ПЛОСКОСТИ.

Например, базисные векторы 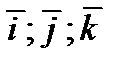некомпланарные.

ОПРЕДЕЛЕНИЕ 4.3. ТРИ УПОРЯДОЧЕННЫХ НЕКОМПЛАНАРНЫХ ВЕКТОРА 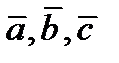С ОБЩИМ НАЧАЛОМ ОБРАЗУЮТ В ТАКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПРАВУЮ ТРОЙКУ ВЕКТОРОВ, ЕСЛИ КРАТЧАЙШИЙ ПОВОРОТ ВЕКТОРА 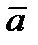К ВЕКТОРУ 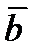, НАБЛЮДАЕМЫЙ ИЗ КОНЦА ВЕКТОРА 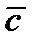, СОВЕРШАЕТСЯ ПРОТИВ ЧАСОВОЙ СТРЕЛКИ.

ОПРЕДЕЛЕНИЕ 4 4. ПУСТЬ ЗАДАНЫ ДВА НЕНУЛЕВЫХ ВЕКТОРА 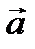И 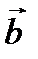ТОГДА ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ 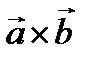НАЗЫВАЕТСЯ ВЕКТОР 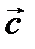, ОПРЕДЕЛЯЕМЫЙ ТРЕМЯ СВОЙСТВАМИ:

1)

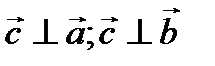
2) ВЕКТОРА 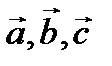ОБРАЗУЮТ ПРАВУЮ ТРОЙКУ ВЕКТОРОВ (4.13)

3) ДЛИНА ВЕКТОРА 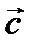ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ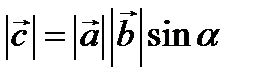

СЛЕДУЮЩИЕ РАВЕНСТВА ЛЕГКО ПРОВЕРИТЬ, ПОЛЬЗУЯСЬ ОПРЕДЕЛЕНИЕМ 4.4

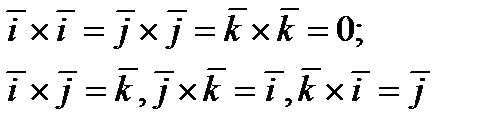
ВЫЧИСЛЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ В КООРДИНАТАХ. ПРАВИЛО .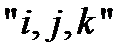

ТЕОРЕМА 4.3 ПУСТЬ ЗАДАНЫ ДВА ВЕКТОРА 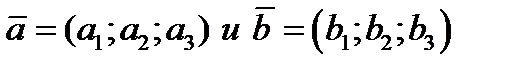, ТОГДА КООРДИНАТЫ

ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ 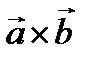ВЫЧИСЛЯЮТСЯ ПО ФОРМУЛЕ 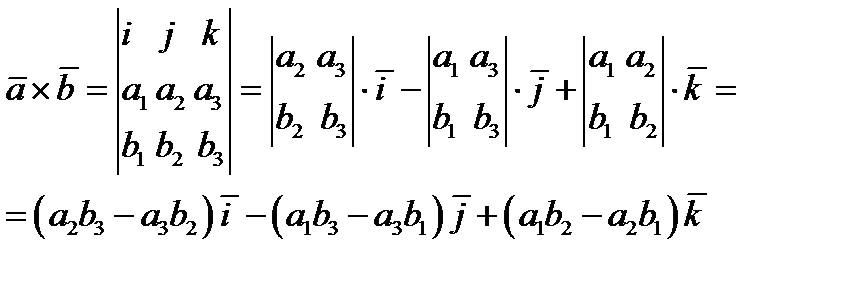(4.14)

ДОКАЗАТЕЛЬСТВО. ПРИ УМНОЖЕНИИ ИСПОЛЬЗУЕМ СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ

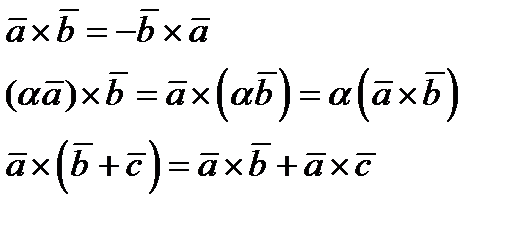(4.15)

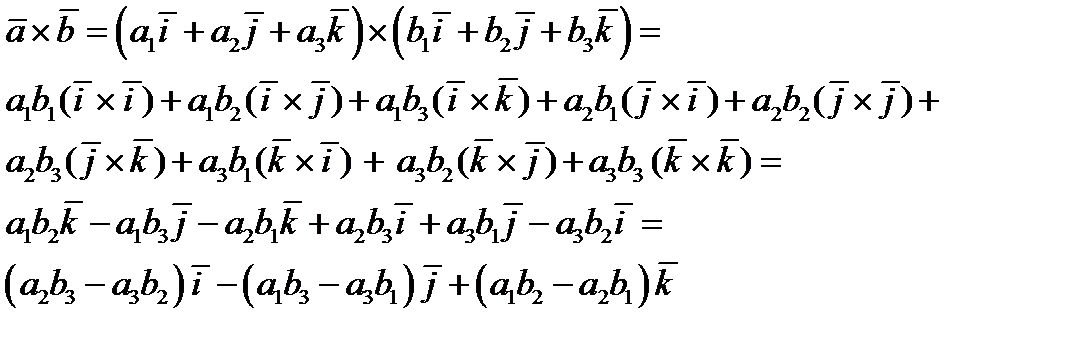
Получили известную формулу вычисления определителя разложением по первой строке.

Теорема доказана.

С помощью векторного произведения можно решать следующие задачи:

1. ВЫЧИСЛЯТЬ ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА, ПОСТРОЕН0ГО НА ВЕКТОРАХ 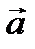И 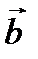КАК НА СТОРОНАХ. ДВУХШАГОВЫЙ АЛГОРИТМ ДАЁТСЯ ФОРМУЛОЙ

(4.16)

1 ШАГ. ВЫЧИСЛЯЕМ ПО ФОРМУЛЕ (4.14) ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ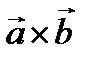

2 ШАГ. НАХОДИМ ДЛИНУ ПОЛУЧЕННОГО ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ПО ФОРМУЛЕ (4.6).

2. ВЫЧИСЛЯТЬ МОМЕНТ СИЛЫ 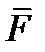, ПРИЛОЖЕНОЙ К ТОЧКЕ 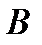, ОТНОСИТЕЛЬНО ТОЧКИ .

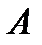СПРАВЕДЛИВА ФОРМУЛА

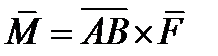(4.17)