Задание 2

Задание 1

Имеются следующие выборочные данные о стоимости основных производственных фондов и выпуске продукции по 30 однородным предприятиям одного из регионов за год, млрд. руб. (выборка 20%-ная, механическая):

Таблица 1.1

Исходные данные

№ предпри-ятия	Среднегодовая стоимость основных производ-ственных фондов	Объем выпуска продукции	№ предпри-ятия	Среднегодовая стоимость основных производ-ственных фондов	Объем выпуска продукции
	19,6	24,4		32,5	33,1
	24,7	28,0		45,8	48,7
	29,3	29,1		43,7	43,1
	31,3	33,6		30,7	30,5
	32,1	35,5		31,3	34,3
	26,7	29,4		42,4	41,8
	28,7	29,5		40,7	41,5
	38,6	36,8		41,1	39,2
	43,2	42,3		33,4	35,4
	49,9	46,9		15,0	25,5
	55,0	50,5		20,3	20,9
	32,2	34,1		24,1	24,5
	32,3	31,5		35,5	37,2
	32,4	30,2		37,7	37,6
	40,7	40,3		33,2	34,5

По исходным данным:

1. Построить статистический ряд распределения предприятий по признаку — Среднегодовая стоимость основных производственных фондов(ОПФ), образовав четыре группы с равными интервалами.

2. Графическим методом и путем расчетов определить значения моды и медианы.

3. Рассчитать характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.

4. Вычислить среднюю арифметическую по исходным данным, сравнить ее с аналогичным показателем, рассчитанным в п. 3 для интервального ряда распределения. Объяснить причину их расхождения.

Сделать выводы по результатам выполнения задания.

1.1

Для построения интервального ряда распределения определяем величину интервала i по формуле:

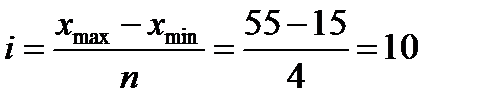млрд. руб.

При i =10 млрд. руб. границы интервалов ряда распределения имеют следующий вид:

Таблица 1.2

Границы интервалов ряда распределения предприятий по признаку среднегодовая стоимость ОПФ

Номер	Нижняя граница	Верхняя граница
группы

Для построения интервального ряда необходимо подсчитать число организаций, входящих в каждую группу (частоты групп).

Процесс группировки единиц совокупности по признаку среднегодовая стоимость ОПФ представлен в таблице 1.3.

Таблица 1.3

Интервальный ряд распределения предприятий по среднегодовой стоимости ОПФ

Группа предприятий по среднегодовой стоимости ОПФ	Число предприятий в группе	Накопительная частота	Накопленная частотноть группы, %
В абсолютном выражении	В процентах к итогу, %
15 - 25		16,67		16,67%
25 - 35		43,33		60,00%
35 - 45		30,00		90,00%
45 - 55		10,00		100,00%
Итого:		100,00		100,00%

Вывод: Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по среднегодовой стоимости ОПФ не является равномерным:

Предприятия с наиболее типичными значениями показателя входят в интервал от 25 млрд. руб. до 35 млрд. руб. Их удельный вес 43,33%.

Предприятия с наибольшими значениями показателя входят в интервал от 45 млрд. руб. до 55 млрд. руб. Их удельный вес 10%.

Предприятия с наименьшими значениями показателя входят в интервал от 15 млрд. руб. до 25 млрд. руб. Их удельный вес 16,67%.

1.2

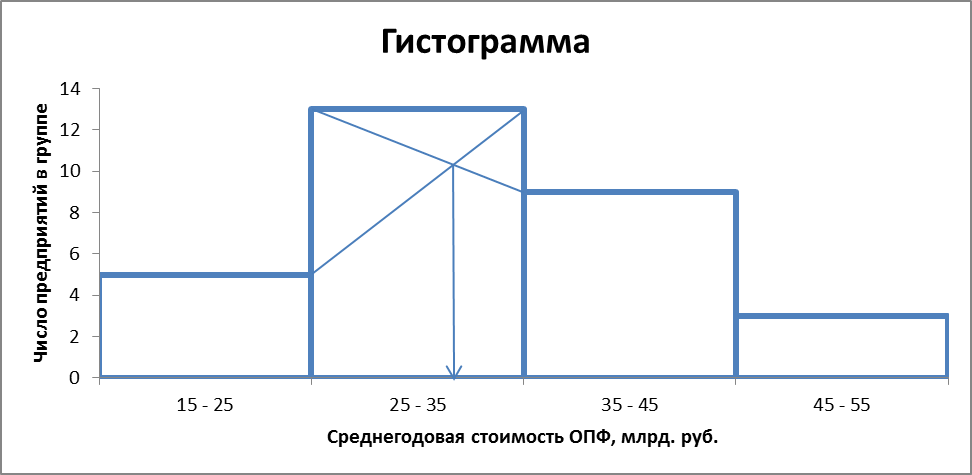
Рис.1.1 Определение моды графическим методом,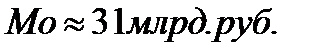

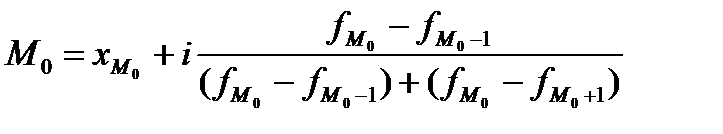,где 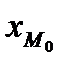- нижняя граница модального интервала; i – величина модального интервала; 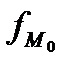- частота модального интервала; 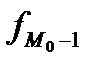- частота интервала, предшествующего модальному; 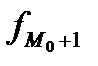- частота интервала, следующего за модальным.

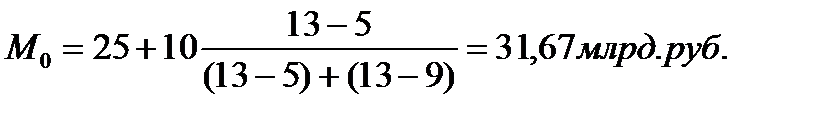
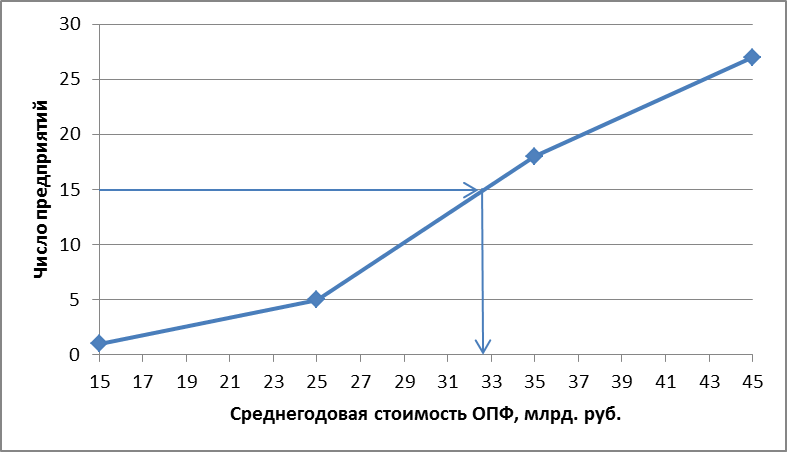
Рис.1.2 Определение медианы графическим методом,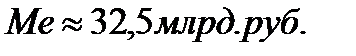

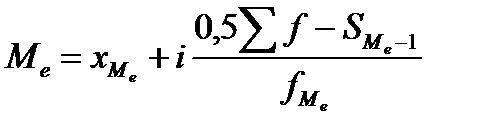,где 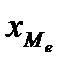- нижняя граница медианного интервала; i – величина медианного интервала; 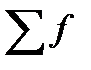- сумма всех частот ряда; 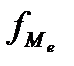- частота медианного интервала; 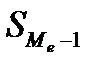- накопительная частота интервала, предшествующая медианному.

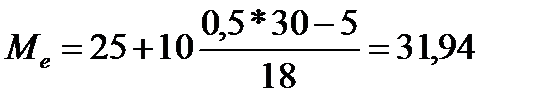
Вывод: Мода ряда распределения равна примерно 31,67 млрд. руб. Она показывает, что в данной совокупности чаще всего встречаются предприятия с уровнем среднегодовой стоимости ОПФ 31,67 млрд. руб.

Медиана ряда распределения равна примерно 31,94 млрд. руб. Она показывает, что в данной совокупности 50% предприятий имеют среднегодовую стоимость ОПФ менее 31,94 млрд. руб., а остальные 50% – более 31,94 млрд. руб.

1.3

Расчет характеристик интервального ряда распределения проведем в рабочей таблице 1.4.

Таблица 1.4

Расчетная таблица для нахождения характеристик ряда распределения.

Группа предприятий по среднегодовой стоимости ОПФ	Число предприятий в группе	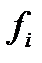Середина интервала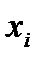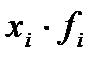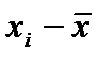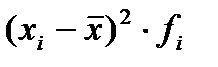
15 - 25		20,0		-13,33	888,89
25 - 35		30,0		-3,33	144,44
35 - 45		40,0		6,67	400,00
45 - 55		50,0		16,67	833,33
Итого					2266,67

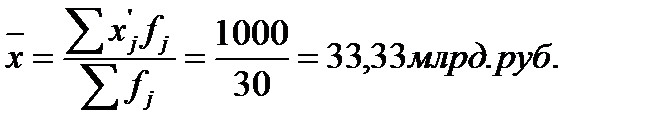
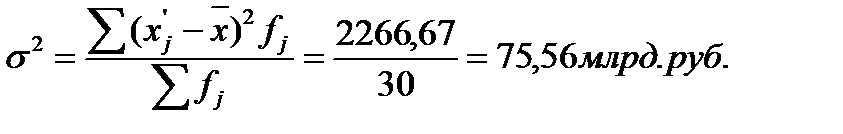
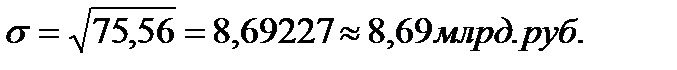
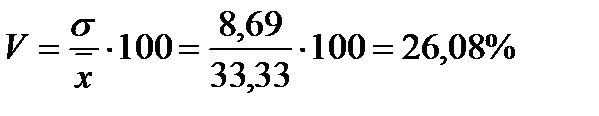
Вывод: На основе проведенных расчетов можно сделать вывод о том, что средний уровень среднегодовой стоимости ОПФ для данной совокупности составляет 33,33 млрд. руб., отклонение от средней в ту или иную сторону составляет в среднем 8,69 млрд. руб. (или 26,08%).

Показатель 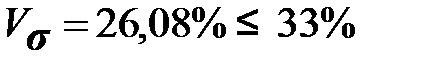, следовательно, по данному признаку выборочная совокупность однородна.

Так как значение показателя лежит в диапазоне 0%<V _s 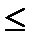40%оценочной шкалы, следовательно, колеблемость изучаемого признака незначительная.

Распределение приблизительно симметрично, так как параметры 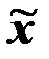, Mo, Me отличаются незначительно:

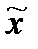=33,33, Mo =31,67, Me =31,94.

Таким образом, найденный средний уровень среднегодовой стоимости ОПФ (33,33 млрд. руб.) является типичной, надежной характеристикой исследуемой совокупности предприятий.

1.4

Для расчета применяется средняя арифметическая простая:

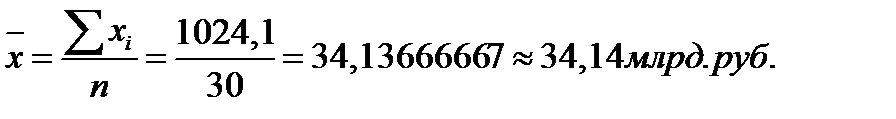
Причина расхождения средних величин заключается в том, что средняя арифметическая по исходным данным определяется по фактическим значениям исследуемого признака для всех 30 предприятий, а средняя арифметическая рассчитанная в п.3 вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов, следовательно, значение средней будет менее точным.

Задание 2

По исходным данным:

1. Установить наличие и характер связи между признаками — Среднегодовая стоимость ОПФ и Объем выпуска продукции методами:

а ) аналитической группировки;

б) корреляционной таблицы.

2. Измерить тесноту корреляционной связи между названными признаками с использованием коэффициентов детерминации и эмпирического корреляционного отношения.

Сделать выводы по результатам выполнения задания.

2.1

Точечный график связи признаков изучаемой совокупности позволяет сделать вывод, что имеет место статистическая связь. Предположительный вид связи – линейная прямая.

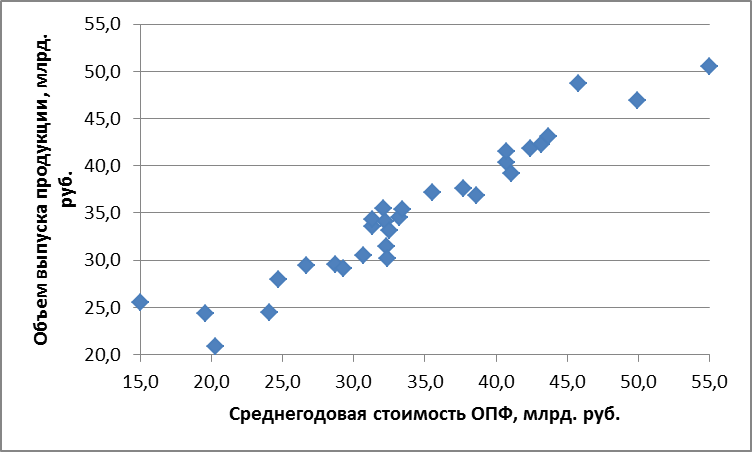
Рис. 2.1 Диаграмма рассеяния

Аналитическая группировка строится по факторному признаку X и для каждой j-й группы ряда определяется среднегрупповое значение результативного признака Y. Если с ростом значений фактора X от группы к группе средние значения систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.

Построим таблицу аналитической группировки, характеризующую зависимость между факторным признаком X – среднегодовая стоимость ОПФ и результативным признаком Y – объем выпуска продукции. Макет аналитической таблицы имеет следующий вид (табл. 2.1).

Таблица 2.1

Зависимость между факторным и результативным признаками

№ группы	Группы предприятий по среднегод. ст-ти ОПФ	Число предприятий в группе	Объем выпуска продукции
Всего	Среднее
	15 - 25		123,3	24,66
	25 - 35		420,7	32,36
	35 - 45		359,8	39,98
	45 - 55		146,1	48,70
Итого			1049,9	35,00

Вывод: Результаты выполнения аналитической группировки предприятий по факторному признаку, представленные в таблице 2.1, показывают, что с увеличением значений факторного признака Х (среднегодовая стоимость ОПФ) закономерно увеличиваются средние групповые значения результативного признака (объем выпуска продукции). Следовательно, между признаками Х и Y существует прямая корреляционная связь.

Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам факторному и результативному. Величина интервала и границы интервалов для факторного признака известны, для результативного признака – Объем выпуска продукции величина интервала определяется по формуле:

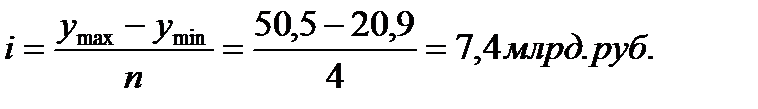
Процесс группировки единиц совокупности по признаку Объем выпуска продукции представлен в таблице 2.2

Таблица 2.2

Интервальный ряд распределения предприятий по объему выпуска продукции

Группа предприятий по объему выпуска продукции	Число предприятий в группе	Накопительная частота	Накопленная частотноть группы, %
В абсолютном выражении	В процентах к итогу, %
20,9 - 28,3		16,67		16,67%
28,3 - 35,7		43,33		60,00%
35,7 - 43,1		30,00		90,00%
43,1 - 50,5		10,00		100,00%
Итого:		100,00		100,00%

Используя группировки по факторному и результативному признакам строим корреляционную таблицу (табл. 2.3)

Таблица 2.3

Корреляционная таблица зависимости между факторным и результативным признаками

Группы предприятий по среднегод. ст-ти ОПФ, млрд. руб.	Группы предприятий по объему выпуска продукции, млрд. руб.
	20,9 - 28,3	28,3 - 35,7	35,7 - 43,1	43,1 - 50,5	Итого
15 - 25
25 - 35
35 - 45
45 - 55
Итого

Вывод: Анализ данных таблицы 2.3 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между Среднегодовая стоимость ОПФ и Объем выпуска продукции.

2.2

Для измерения тесной связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации 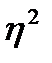и эмпирическое корреляционное отношение .

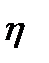Эмпирический коэффициент детерминации рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле:

,

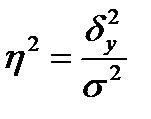где 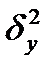- межгрупповая дисперсия результативного признака;

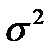- общая дисперсия результативного признака.

,

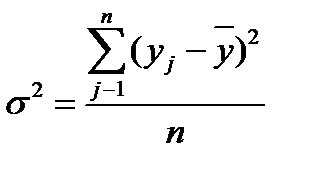где 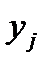- индивидуальное значение результативного признака;

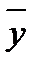- общее среднее значение результативного признака;

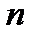- число единиц совокупности.

,

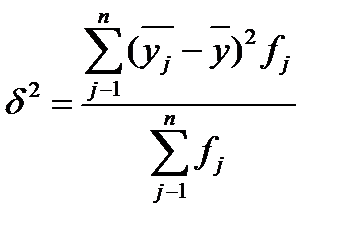где 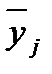- групповые средние;

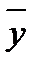- общая средняя;

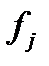- число единиц в 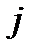-ой группе;

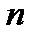- число групп.

Общая средняя 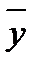вычисляется как средняя арифметическая простая по всем единицам совокупности:

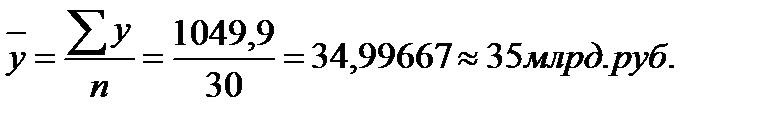
Для расчета общей дисперсии 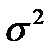применяется вспомогательная таблица 2.4.

Таблица 2.4

Вспомогательная таблица для расчета общей дисперсии

№ предприятия	Объем выпуска продукции, млн.руб.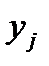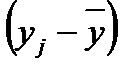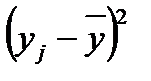
	20,9	-14,1	198,81
	24,4	-10,6	112,36
	24,5	-10,5	110,25
	25,5	-9,5	90,25
	28,0	-7,0	49,00
	29,1	-5,9	34,81
	29,4	-5,6	31,36
	29,5	-5,5	30,25
	30,2	-4,8	23,04
	30,5	-4,5	20,25
	31,5	-3,5	12,25
	33,1	-1,9	3,61
	33,6	-1,4	1,96
	34,1	-0,9	0,81
	34,3	-0,7	0,49
	34,5	-0,5	0,25
	35,4	0,4	0,16
	35,5	0,5	0,25
	36,8	1,8	3,24
	37,2	2,2	4,84
	37,6	2,6	6,76
	39,2	4,2	17,64
	40,3	5,3	28,09
	41,5	6,5	42,25
	41,8	6,8	46,24
	42,3	7,3	53,29
	43,1	8,1	65,61
	46,9	11,9	141,61
	48,7	13,7	187,69
	50,5	15,5	240,25
Итого	1049,9	Итого	1557,67

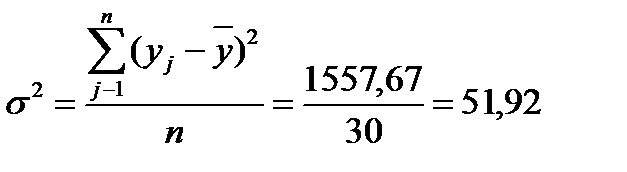
Для расчета межгрупповой дисперсии строится вспомогательная таблица 2.5.

Таблица 2.5

Вспомогательная таблица для расчета межгрупповой дисперсии.

Группы предприятий по объему выпуска продукции	Число предприятий в группе	Среднее значение в группе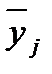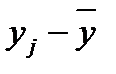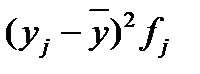
20,9 - 28,3		24,6	-10,4	540,80
28,3 - 35,7		32,0	-3,0	117,00
35,7 - 43,1		39,4	4,4	174,24
43,1 - 50,5		46,8	11,8	417,72
Итого			Итого	1249,76

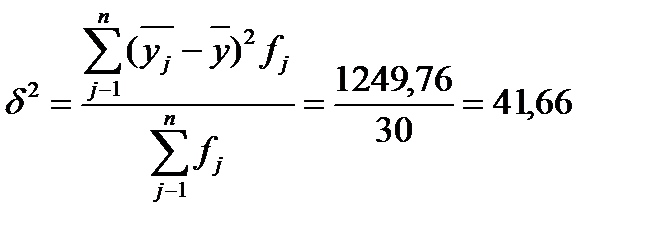
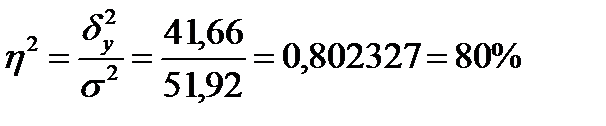
Вывод: Эмпирический коэффициент детерминации показывает, что 80% вариации объема выручки от продаж обусловлено уровнем среднегодовой стоимости основных производственных фондов, а 20% - влиянием прочих неучтенных факторов.

Эмпирическое корреляционное отношение 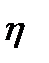оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле:

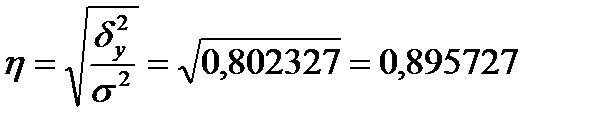или 89,6%

Вывод: Согласно шкале Чэддока связь между факторным и результативным признаками совокупности является тесной.

Задание 3

По результатам выполнения задания 1 с вероятностью 0,954 определить:

1. Ошибку выборки среднего уровня среднегодовой стоимости ОПФ и границы, в которых будет находиться средний уровень среднегодовой стоимости ОПФ для генеральной совокупности предприятий;

2. Ошибку выборки доли предприятий с уровнем среднегодовой стоимости ОПФ35 млрд.руб. и более и границы, в которых будет находиться генеральная доля.

3.1

Средняя ошибка выборки 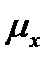- это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней.

Для случайной и механической выборки с бесповторным способом отбора средняя ошибка 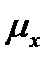выборочной средней 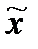определяется по формуле:

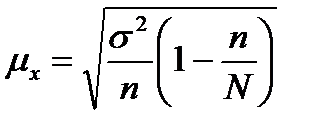
Предельная ошибка выборки 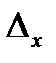определяет границы, в пределах которых будет находиться генеральная средняя:

,

,

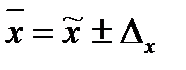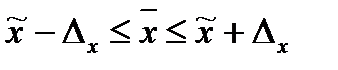где 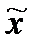- выборочная средняя;

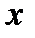-генеральная средняя.

Предельная ошибка выборки кратна средней ошибке с коэффициентом кратности t (называемым коэффициентом доверия):

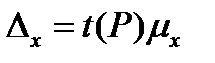
Наиболее часто используемые доверительные вероятности Р и соответствующие им значения t задаются следующим образом (табл. 3.1)

Таблица 3.1

Доверительная вероятность P	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

По условию выборочная совокупность насчитывает 30 предприятий, выборка 20%-ная механическая, следовательно, генеральная совокупность включает 150 предприятий. Значение параметров, необходимых для решения задачи, представлены в таблице 3.2.

Таблица 3.2

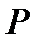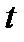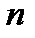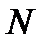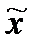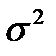0,954	2,0			33,33	75,56

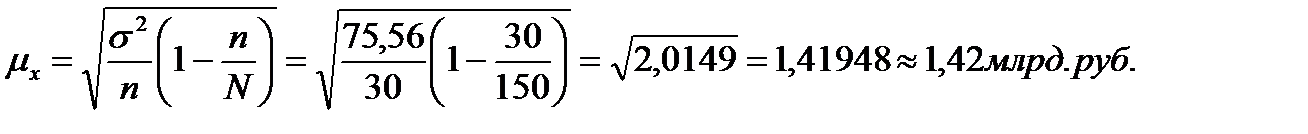
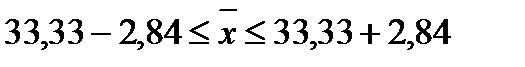
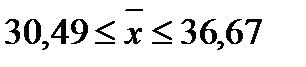
Вывод: На основании предельного выборочного обследования предприятий с вероятностью 0,954 можно утверждать, что для генеральной совокупности предприятий средний уровень среднегодовой стоимости ОПФ находится в пределах от 30,49 млрд. руб. до 36,67 млрд. руб.

3.2

Доля выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой:

,

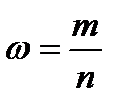где 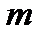- число единиц совокупности, обладающих заданным свойством;

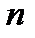- общее число совокупностей.

Для случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 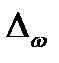доли единиц, обладающих заданным свойствам, рассчитывается по формуле:

,

,

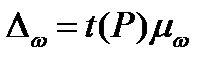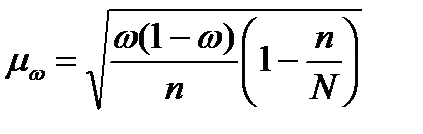где 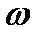- доля единиц совокупности, обладающих заданным свойствам;

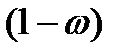- доля единиц совокупности, не обладающих данным свойством;

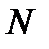- число единиц в генеральной совокупности;

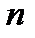- число единиц в выборочной совокупности.

Предельная ошибка выборки 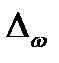определяет границы, в пределах которых будет находиться генеральная доля 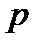единиц, обладающих заданным свойством:

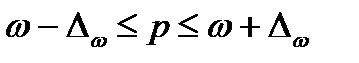
По условию задания исследуемым свойством является равенство или превышающий 35 млрд. руб. уровень среднегодовой стоимости ОПФ. Число предприятий с заданным свойством определяется из таблицы 1.3 (графа 2).

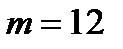
Расчет выборочной доли:

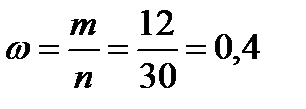
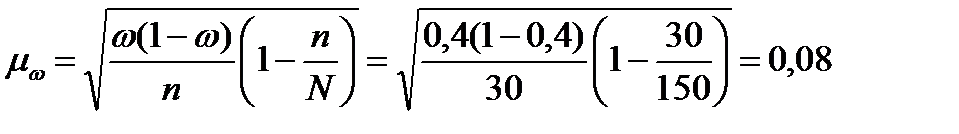
Расчет предельной ошибки выборки для доли:

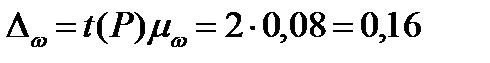
Определение доверительного интервала генеральной доли:

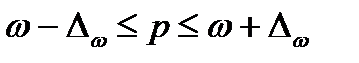
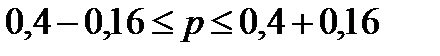
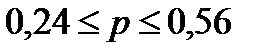
или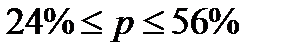

Вывод: С вероятностью 0,954 можно утверждать, что в генеральной совокупности предприятий доля предприятий с уровнем среднегодовой стоимости ОПФ 35 млрд. руб. и выше будет находиться в пределах от 24% до 56%.