2015-10-16
479
· Закон всемирного тяготения
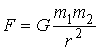, (9.1)
где F – сила взаимного притяжения двух материальных точек;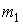 
и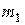 
– их массы; r – расстояние между точками; G – гравитационная постоянная, равная 
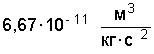.В указанной формуле закон всемирного тяготения можно применить и к взаимодействию шаров, масса которых распределена сферически – симметрично. В этом случае r есть расстояние между центрами шаров.
· Напряженность гравитационного поля
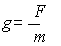, (9.2)
где F – сила тяготения, действующая на материальную точку массы 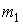, помещенную в некоторую точку поля.
Напряженность гравитационного поля, создаваемого планетой, массу M которой можно считать распределенной сферически – симметрично:
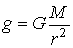, (9.3)
где r – расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
· Ускорение свободного падения на высоте h над поверхностью Земли
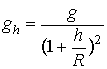, (9.4)
где R – радиус Земли; g – ускорение свободного падения на поверхности Земли. Если h<<R, то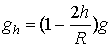 
.
· Потенциальная энергия гравитационного взаимодействия двух материальных точек массам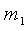и 
и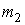 
(шаров с массой, распределенной сферически, – симметрично), находящихся на расстоянии r друг от друга:
|
|
|
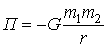, (9.5)
(потенциальную энергию бесконечно удаленных друг от друга материальных точек принято считать равной нулю).
· Потенциал гравитационного поля
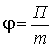, (9.6)
где П – потенциальная энергия точки массой m, помещенной в данную точку поля.
· Потенциал гравитационного поля, создаваемого планетой, массу M которой можно считать распределенной сферически – симметрично:
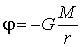, (9.7)
где r – расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
