Ускорение точки характеризует изменение ее скорости в рассматриваемой системе отсчета с течением времени.
4.4.1. Векторный способ. Пусть за время D t точка переместилась из положения M, где она имела скорость 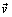 , в положение
, в положение 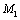 , где ее скорость стала равной
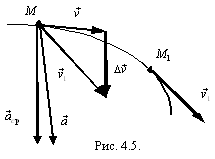
, где ее скорость стала равной 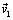 (рис. 4.5). Вектор скорости получил приращение
(рис. 4.5). Вектор скорости получил приращение 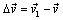 . Средним ускорением точки за интервал времени D t называют отношение
. Средним ускорением точки за интервал времени D t называют отношение 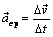 . Предел среднего ускорения
. Предел среднего ускорения
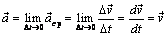 (4.12)
(4.12)
 называют ускорением точки в данный момент времени или просто ускорением точки.
называют ускорением точки в данный момент времени или просто ускорением точки.
Таким образом, ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости точки в рассматриваемой системе отсчета. Так как 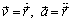 Вектор среднего ускорения лежит в плоскости, образуемой векторами
Вектор среднего ускорения лежит в плоскости, образуемой векторами 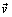 и
и 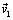 . При уменьшении D t точка
. При уменьшении D t точка 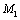 приближается к точке М, и плоскость векторов
приближается к точке М, и плоскость векторов 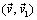 изменяет свое положение в пространстве, поворачиваясь вокруг вектора
изменяет свое положение в пространстве, поворачиваясь вокруг вектора 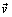 . Предельное положение этой плоскости называют соприкасающейся плоскостью кривой в точке М (см. рис. 4.2, плоскость М t n). Следовательно, вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории (см. рис. 4.5).
. Предельное положение этой плоскости называют соприкасающейся плоскостью кривой в точке М (см. рис. 4.2, плоскость М t n). Следовательно, вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории (см. рис. 4.5).
Единица измерения ускорения в системе СИ – 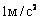 .
.
4.4.2. Координатный способ. Представим вектор скорости в виде 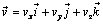 . Тогда, учитывая неизменность ортов
. Тогда, учитывая неизменность ортов 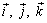 , в соответствии с формулой (4.12) получим ускорение
, в соответствии с формулой (4.12) получим ускорение
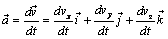
и его проекции:
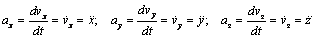 . (4.13)
. (4.13)
По проекциям ускорения определим его модуль
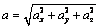 (4.14)
(4.14)
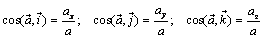 . (4.15)
. (4.15)
4.4.3. Естественный способ. Представим вектор скорости в виде (4.11) 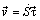 , тогда из формулы (4.12) получим
, тогда из формулы (4.12) получим
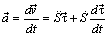 . (4.16)
. (4.16)
Определим модуль и направление вектора 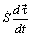 , для чего рассмотрим два случая.
, для чего рассмотрим два случая.
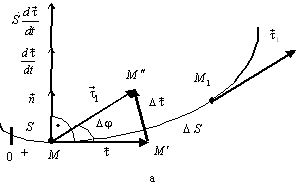
Случай 1. Точка М движется в сторону увеличения координаты S (рис. 4.6,а). За время D t она перемещается из положения М в положение 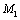 , при этом ее координата увеличивается на величину D S, а вектор
, при этом ее координата увеличивается на величину D S, а вектор 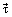 получает приращение
получает приращение 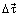 , направленное в сторону вогнутости траектории. Вектор
, направленное в сторону вогнутости траектории. Вектор 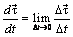 направлен перпендикулярно вектору
направлен перпендикулярно вектору 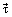 в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Вектор
в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Вектор 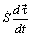 имеет такое же направление, так как координата S возрастает, при этом
имеет такое же направление, так как координата S возрастает, при этом 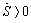 .
.
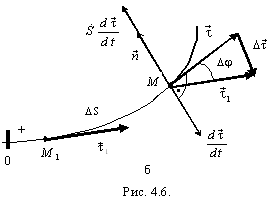
Случай 2. Точка М движется в сторону уменьшения координаты S (рис. 4.6,б). Вектор 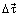 , а вместе с ним и вектор
, а вместе с ним и вектор 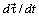 , направлены в сторону выпуклости траектории. Вектор
, направлены в сторону выпуклости траектории. Вектор 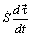 имеет противоположное направление, так как
имеет противоположное направление, так как 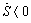 . Таким образом, вектор
. Таким образом, вектор 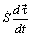 всегда направлен по главной нормали к траектории в сторону вогнутости и может быть представлен в виде:
всегда направлен по главной нормали к траектории в сторону вогнутости и может быть представлен в виде:
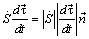 . (4.17)
. (4.17)
 |
 |
Определим модуль вектора 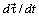 . Учитывая, что
. Учитывая, что 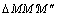 равнобедренный (см. рис. 4.6,а) и
равнобедренный (см. рис. 4.6,а) и 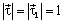 , получим
, получим
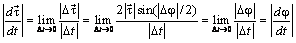 . (4.18)
. (4.18)
Из формул (4.17) и (4.18) следует
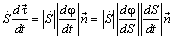 .
.
откуда, учитывая, что 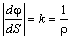 , где k – кривизна, а ρ – радиус кривизны траектории в данной точке, получим
, где k – кривизна, а ρ – радиус кривизны траектории в данной точке, получим
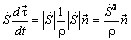 . (4.19)
. (4.19)
Подставим (4.19) в (4.16)
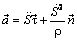 . (4.20)
. (4.20)
Таким образом, вектор ускорения имеет две составляющие: касательную и нормальную.
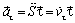 (4.21)
(4.21)
направлено по касательной к траектории в сторону увеличения координаты S, если алгебраическая скорость точки 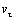 возрастает, или в сторону уменьшения S, если
возрастает, или в сторону уменьшения S, если 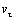 убывает. Проекция касательного ускорения на ось t:
убывает. Проекция касательного ускорения на ось t:
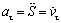 . (4.22)
. (4.22)
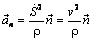 (4.23)
(4.23)
всегда направлено по нормали к траектории в сторону вогнутости, его проекция на ось n:
 . 4.24)
. 4.24)
Так как 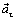 ^
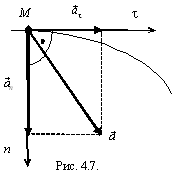
^ 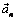 (рис. 4.7), модуль вектора ускорения находим по формуле
(рис. 4.7), модуль вектора ускорения находим по формуле
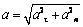 . (4.25)
. (4.25)
Касательное ускорение характеризует изменение скорости точки по модулю, а нормальное – по направлению.
 Касательное ускорение равно нулю:
Касательное ускорение равно нулю:
1) если точка движется с постоянной алгебраической скоростью;
2) в те моменты времени, когда скорость 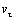 принимает экстремальные значения.
принимает экстремальные значения.
Нормальное ускорение равно нулю:
1) при прямолинейном движении (r = ¥);
2) в точках перегиба траектории (r = ¥);
3) в те моменты времени, когда скорость точки равна нулю.
 2015-10-14
2015-10-14 971
971








