Нахождение средней арифметической генеральной совокупности

Основная задача выборочного метода — определение средней арифметической генеральной совокупности _ген. без исследования всех объектов ее объема. Для решения такой задачи необходимо составить выборку, репрезентатирующую данную генеральную совокупность. В полученной выборке найти ее среднюю арифметическую _выб.

Установлено, что, если выборочная совокупность достаточно хорошо представляет генеральную, средняя арифметическая выборки _выб репрезентатирует среднюю арифметическую генеральной совокупности _ген. При этом, однако, следует учесть два обстоятельства: во-первых, средняя выборки _выб не может быть точно равна средней генеральной совокупности _ген., а отличается от нее. Отличие это носит принципиальный характер, так как какой бы репрезентативной не была выборка, ее объем меньше объема генеральной и, таким образом, подобный анализ не может отразить истинного существа дела. Отличие средних арифметических _ген. и _выб. может быть, конечно, большим или меньшим, что зависит от многих условий. Например, выше было указано, что выборка тем репрезентативней, чем больший объем она имеет. Следовательно, чем больше объем выборочной совокупности, тем точнее выборка представляет генеральную и тем меньше должно быть различие в средних _ген. и _выб.

Во-вторых, говоря о характеристике средней арифметической генеральной _ген. посредством выборочной _выб., следует говорить о вероятности, с которой гарантируется определенная точность счета.

В связи с этим. в рассматриваемой задаче существуют два основных понятия: ошибка репрезентативности m и надежность Р (или еще говорят: доверительная вероятность) и ее характеристика—критерий надежности t.

Ошибка репрезентативности указывает на величину различия между средними арифметическими генеральной и выборочной совокупностей.

Определить ошибку репрезентативности можно двумя способами.

1. Если выборочная совокупность составлена таким образом, что любой объект генеральной может попасть в выборку несколько раз (см. первый способ образования выборки), то ошибку репрезентативности можно определить по формуле:

где m — ошибка репрезентативности.;

s _выб — среднее квадратическое отклонение выборочной совокупности;

n — объем выборки.

Более точной является формула:

где (n—1) представляет собой так называемое число степеней свободы.

Число степеней свободы есть количество вариантов, принимающих произвольные значения, не меняющие величину средней арифметической.

При объемах выборки n=30 различие между n и (n—1) практически не ощущается, вследствие чего можно пользоваться любой из формул (20) или (21). При выборках численностью менее 30 такое различие более ощутимо. В этом случае предпочтительна формула (21).

2. Если выборка образована из генеральной таким образом, что любой объект генеральной совокупности не может быть в ней повторим (см. второй способ образования выборочной совокупности), ошибка может быть определена по формуле:

где m — ошибка репрезентативности;

s _выб.—среднее квадратическое отклонение выборочной совокупности;

n — объем выборки;

N — объем генеральной совокупности.

Совершенно очевидно, что, пользуясь формулой (22), необходимо знать численность генеральной совокупности N, без чего можно обойтиcь в формулах (20) и (21). Отсюда следует, что если численность генеральной неизвестна, как это часто имеет место в спортивных работах, выборочную совокупность нужно отбирать посредством первого способа и пользоваться формулами (20) и (21).

Найденная любым из приведенных способов ошибка репрезентативности фактически покажет, как мы ошиблись в определении средней арифметической _ген., когда вместо генеральной совокупности рассматривали выборочную. Как уже было отмечено выше, такая ошибка носит не случайный, а принципиальный характер.

Представим себе, что нами установлена величина ошибки репрезентативности. Ее определение могло быть более точным или менее точным. Желательно знать не только величину абсолютного расхождения между средними арифметическими генеральной и выборочной совокупностей, но и определить каким-либо образом точность произведенного расчета. Характеристикой такой точности является надежность.

Надежность (доверительная вероятность) есть вероятность, с которой гарантируется точность расчетов при определении генеральной средней (посредством выборочной). Поскольку число, выражающее вероятность в соответствии с определением вероятности, не выходит за пределы единицы, надежность, выраженная числом, естественно, меньшим единицы, может быть дополнена до единицы, так сказать, «оставшейся» вероятностью. Такая вероятность называется уровнем значимости b.

Например, если надежность есть Р=0,95, то дополнением до полной вероятности, равной единице, есть величина 0,05. Таким образом, уровень значимости здесь b=0,05.

В рассматриваемой задаче до начала вычислений задают надежность, необходимую для данных исследований (или, что то же, — задают уровень значимости). Как правило, надежность на должном уровне обеспечивается достаточным объемом выборки. Вследствие этого, надежность и объем выборочной совокупности должны быть взаимно увязаны.

Английский статистик Стьюдент исследовал эту взаимосвязь на основании свойств нормального закона. Результаты его исследований представляют собой очень подробную таблицу, где каждому значению надежности соответствует объем выборочной совокупности. Это соответствие соблюдается также по исследованиям Стьюдента и в отношении критерия надежности t —не которой характеристики надежности счета.

Таким образом, таблица Стьюдента представляет собой информацию по определению критерия надежности и объема выборки, соответствующих определенной надежности (см. приложение 2).

Какой же надежностью следует пользоваться в спортивных исследованиях? Специальных указаний по этому поводу дать, конечно, нельзя. Исследователь волен в избрании надежности для конкретной задачи, он только вынужден обеспечить объем выборки, соответствующий избранной надежности, пользуясь таблицей Стьюдента.

Тем не менее, можно указать на несколько значений надежностей, принимаемых во многих исследованиях спорта. Считается достаточно высокой для точности и необременительной по объему выборки надежность р₁=0,95. Это самое распространенное значение надежности, применяемое для расчетов в многочисленных спортивных задачах широкого класса.

Надежность Рз=0,99 принимается в спорте реже. Здесь речь идет о повышенных требованиях точности, могущих иметь место при доказательстве какой-либо фундаментальной теории или теста, при разрешении какой-либо проблемы, связанной с предпочтительностью однотипных изысканий и т. д.

Наконец, очень редко в спорте встречается третье значение надежности Рз=0,999. Как правило, это или медицинские работы, связанные с лечением и примене­нием лечебных средств, или работы, связанные с иссле­дованием больших перегрузок в спорте—в обоих этих случаях речь идет о жизни и здоровье людей, поэтому высокая точность счета оправдана при любых обстоятельствах, даже если исходные данные неточны в сравнении с методами их обработки. Для этих трех надежностей объем выборки и критерии надежности находим по таблице Стьюдента (табл. 39).

Таблица 39

Надежность	Критерии надежности	Объем выборки
Р=0,95 Р2=0,99 Рз= 0,999	t1=2,04(»2,0) t2=2,75 t3=3.65	n1>30 n2>30 n3>30

Попутно обратим внимание на то, что численность выборки n=30, предложенная ранее, способна гарантировать нужные для расчета надежности.

Возвратимся к задаче определения средней арифметической генеральной совокупности посредством выборочной. Для определения искомой _ген, выборочный метод предлагает определить границы, называемые нижним и верхним доверительными интервалами, в пределах которых должна находиться средняя арифметическая генеральной совокупности.

Формула определения _ген. выглядит так:

_выб — (mt) < _ген. < _выб + (mt). (23)

где _ген. — средняя арифметическая генеральной совокупности;

_выб. — (mt) — нижняя доверительная граница;

_выб. + (mt) — верхняя доверительная граница;

от [ _выб. — (mt)] до [ _выб.+(mt)]—доверительный интервал;

_выб. — средняя арифметическая выборочной совокупности;

m — ошибка репрезентативности;

t — критерий надежности.

Иногда произведение (mt) называют абсолютной погрешностью, как некоторый общий показатель ошибки репрезентативности и надежности.

Таким образом, для определения средней арифметической генеральной совокупности, составляем выборку, исследуем ее обычным методом средних величин, находим по одной из вышеприведенных формул ошибку репрезентативности, задавшись надежностью, находим критерий надежности по таблице Стьюдента. Полученные данные подставляем в формулу (23) и находим те пределы, в которых должна находиться искомая средняя арифметическая генеральной совокупности. При помощи этого метода получим информацию о генеральной совокупности, не исследуя ее объектов, а перенося ее с определенной степенью точности с выборочной совокупности.

Отсюда следует, что при эмпирических распределениях, соответствующих нормальному закону, найденные выборочным методом величины _ген. и s_ген. могут дать весьма полное представление о всей генеральной совокупности.

Рассмотрим примеры по определению доверительных границ.

Пример 27. В школе 730 мальчиков 14 лет. Из них у группы школьников в 50 человек исследована на силу ног по количеству приседаний в течение 20 с.

По результату исследований этих 50 школьников можно сделать вывод о средних возможностях 730.

х_i —количество приседаний за 20 с.

n_i —количество школьников, показавших данный результат.

Результаты обработаны методом средних величин в табл. 40:

Таблица 40

xi	ni	xini	xi-	(xi- )2	(xi- )2ni
			-4
			—3
			-2
			—1
			+1
			+2
			+3
			+4
	n=50

В соответствии с формулой (22), т.к. известно N определяем величину ошибки репрезентативности:

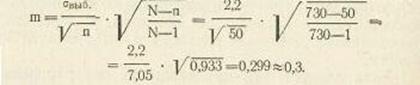
Найденная ошибка m=0,3 свидетельствует о том, что величину _ген — среднюю арифметическую количества приседаний 730 школьников — также можно принять _ген.=13,0, как и у 50 школьников _выб=13,0. Однако при этом погрешность такого предположения составит 0,3 приседания.

Зададимся надежностью P₁=0,95, которой по таблице Стьюдента соответствует критерий надежности t»2,0. Находим величину (mt) — абсолютную погрешность счета: mt=0,3·2,0»0,6.

Нижняя доверительная граница [ _выб—(mt)] =13,0—0,6 ==12,4»12,0. Верхняя доверительная граница [ _выб.+(mt)] =13,0+0.6= 13,6»14.0.

Таким образом, средние возможности 730 школьников находятся в пределах: 12,0< _ген.<14,0, то есть от 12 до 14 приседаний в течение 20 с.

Напомним здесь еще раз о некоторой академичности подобных примеров: числа здесь округляются и рассматривается небольшое их количество, практически же подлежит расчету значительно большее число вариантов.

Пример 28. 42 гандболистки третьего разряда в возрасте 16 лет выполняют бросок мяча на дальность. В катах пределах лежит значение дальности полета мяча у гандболисток третьего разряда 16 лет, если результаты исследованных спортсменок следующие (табл. 41). х_i —дальность полета мяча в метрах;

n_i — количество спортсменок, показавших данный результат.

Таблица 41

xi	ni	xini	xi-	(xi- )2	(xi- )2ni
17,10		85,50	—2,1	4,41	22,05
18,50		74.00	—0,7	0,49	1,96
19,00		266,00	-0,2	0,04	0.56
19,20		211,20
21,30		127,80	+2,1	4,41	26,46
22,00		44,00	+2,8	7,84	15,68
	n=42	808,50			66,71

В соответствии с формулой (21) находим ошибку репрезентативности:

Это говорит о том, что возможности гандболисток третьего разряда 16 лет составляли в среднем: _ген.» _выб.» 19,2 м. Однако, сделав такое предположение, мы ошиблись на 0,2 м.

Задавшись надежностью P₁=0,95, находим критерий надежности t₁=2,0 по таблице Стьюдента. Далее находим абсолютную погрешность mt=0,2 м × 2,0=0,4 м.

Нижняя доверительная граница [ _выб.—(mt)]=19,2 м-0,4 м=18,8 м. Верхняя доверительная граница [ _выб.+(mt)]==19,2 м+0,4 м=19,6 м. Таким образом, искомая величина _ген лежит в пределах: 18,8 < _ген < 19,6 м. Другими словами, на основании приведенные сведений о 42 гандболистках можно сделать вывод о том, что среднее значение дальности полета мяча у гандболисток третьего разряда 16 лет заключается в пределах от 18,8 м до 19,6 м.

В заключение следует сказать, что задача о нахождении средней арифметической генеральной совокупности по выборочной есть одна из возможных. Существуют, например, задачи, где объектом поиска служит доверительная вероятность и др.