Предел функции в бесконечности

Число А называется пределом функции y = f(х) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число S (зависящее от e, т.е. S = S(e)), что для всех х таких, что |х| > S, верно неравенство: |f(x) - А| < e.

Отметим, что отличие этого определения от определения предела последовательности состоит в том, что для последовательности переменная n принимала только натуральные значения, а здесь х принимает любые значения.

Предел функции в бесконечности обозначается или
f(x) ® А при x ® ¥.

Итак, .

Смысл определения состоит в том, что для достаточно больших по модулю значениях аргумента значения функции как угодно мало отличаются от числа А по абсолютной величине. Геометрический смысл определения можно пояснить рисунком 2.3.

Рисунок 2.3 – Геометрический смысл предела функции в бесконечности

Итак, число А есть предел функции у = f(x) при x ® ¥, если для любого e > 0 найдется такое число S > 0, что для всех х таких, что |х| > S, соответствующие ординаты графика функции f(x) будут заключены в e-окрестности точки А на оси ординат. При этом соответствующая часть графика будет находиться в полосе шириной 2e.

Понятие предела функции в бесконечности можно сформулировать и при стремлении х к бесконечности определенного знака. Отличие будет состоять в том, что аргумент функции неограниченно возрастает не по абсолютной величине, а x ® +¥ (тогда в определении вместо |х| > S будет стоять неравенство х > S) либо x ® -¥ (тогда в определении вместо |х| > S будет стоять неравенство х < -S).

Предел функции в точке

Число А называется пределом функции y = f(x) при х, стремящемся к х₀ (или в точке х₀), если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число d (зависящее от e, т.е. d = d (e)), что для всех х ¹ х₀ таких, что |х - х₀| < d, верно неравенство: |f(x) - А| < e.

Предел функции в точке х₀обозначается или
f(x) ® А при x ® х₀.

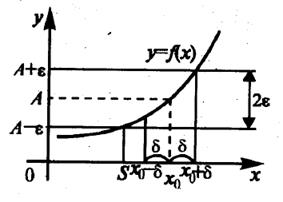
Смысл определения состоит в том, что для всех значений аргумента, достаточно близких к х₀, значения функции как угодно мало отличаются от числа А по абсолютной величине. Геометрический смысл определения можно пояснить рисунком 2.4.

Рисунок 2.4 – Геометрический смысл предела функции в точке

Итак, число А есть предел функции у = f(x) при x ® х₀, если для любого e > 0 найдется такая d-окрестность точки х₀, что для всех х ¹ х₀ из этой окрестности соответствующие ординаты графика функции f(х) будут заключены в e-окрестности точки А на оси ординат. При этом соответствующая часть графика будет находиться в полосе шириной 2e.

Подчеркнем, что определение предела не требует существования функции в самой точке х₀. Рассматривая предел, предполагают, что х стремится к х₀, но не достигает этого значения. Поэтому наличие или отсутствие предела определяется поведением функции в окрестности точки х₀, а не тем, определена или нет функция в самой этой точке.

Понятие предела функции в точке можно сформулировать и в смысле одностороннего предела. Отличие будет состоять в том, что аргумент функции принимает лишь значения x < x₀ (тогда в определении вместо
|х - х₀| < d рассматривается интервал х₀ - d < x < х₀, а предел называют пределом слева и обозначают ) либо лишь значения x > x₀ (тогда в определении вместо |х - х₀| < d рассматривается интервал х₀ < x < х₀+ d, а предел называют пределом справа и обозначают ).

Если 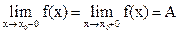, то , и наоборот (т.е. если в некоторой точке функция имеет пределы слева и справа, и они равны, то двусторонний предел тоже существует и равен тому же числу; и наоборот, - если существует двусторонний предел, то существуют и односторонние, равные ему же).