Через данную точку  проходит единственная прямая
проходит единственная прямая  , параллельная данному ненулевому вектору
, параллельная данному ненулевому вектору  . Вектор
. Вектор  , как и любой другой ненулевой вектор, параллельный прямой
, как и любой другой ненулевой вектор, параллельный прямой  , называется направляющим вектором прямой.
, называется направляющим вектором прямой.
Итак, всякая прямая однозначно определяется точкой и направляющим вектором.
Пусть на плоскости задан аффинный репер  и
и  ,
,  . Точка
. Точка  принадлежит прямой
принадлежит прямой  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 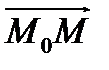 и
и  коллинеарны, то есть отличаются друг от друга числовым множителем:
коллинеарны, то есть отличаются друг от друга числовым множителем:  . Переходя к координатам, найдем уравнения, которым должны удовлетворять координаты
. Переходя к координатам, найдем уравнения, которым должны удовлетворять координаты  точки, принадлежащей прямой:
точки, принадлежащей прямой:
 – параметрические уравнения прямой.
– параметрические уравнения прямой.
Векторы 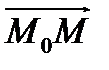 и
и  коллинеарны тогда и только тогда, когда их координаты пропорциональны. Имеем
коллинеарны тогда и только тогда, когда их координаты пропорциональны. Имеем
 – каноническое уравнение прямой.
– каноническое уравнение прямой.
Через данную точку  проходит единственная прямая
проходит единственная прямая  , перпендикулярная данному ненулевому вектору
, перпендикулярная данному ненулевому вектору 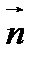 . Вектор
. Вектор 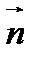 , как и любой другой ненулевой вектор, перпендикулярный прямой
, как и любой другой ненулевой вектор, перпендикулярный прямой  , называется нормальным вектором прямой.
, называется нормальным вектором прямой.
Итак, всякая прямая на плоскости однозначно определяется точкой и нормальным вектором.
Точка  принадлежит прямой
принадлежит прямой  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 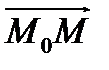 и
и  ортогональны, то есть их скалярное произведение равно нулю. Чтобы использовать координаты векторов, необходим ортонормированный базис, а значит, на плоскости должна быть задана прямоугольная система координат
ортогональны, то есть их скалярное произведение равно нулю. Чтобы использовать координаты векторов, необходим ортонормированный базис, а значит, на плоскости должна быть задана прямоугольная система координат  . Пусть
. Пусть  ,
,  . Выразив условие ортогональности векторов
. Выразив условие ортогональности векторов 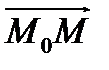 и
и  через координаты, получим уравнение прямой
через координаты, получим уравнение прямой  :
:
 .
.
Выводы:
1. Чтобы составить уравнение прямой, надо знать точку и направляющий вектор, либо точку и нормальный вектор.
2. Уравнение прямой приводится к виду  , где
, где  , – общее уравнение прямой, то есть прямая является алгебраической линией первого порядка.
, – общее уравнение прямой, то есть прямая является алгебраической линией первого порядка.
Т е о р е м а. Любая алгебраическая линия первого порядка является прямой.
Д о к а з а т е л ь с т в о. Для алгебраической линии первого порядка существует аффинная система координат, относительно которой линия задается уравнением  , где
, где  . Пусть
. Пусть  . Приведя уравнение линии к виду, напоминающему каноническое уравнение прямой
. Приведя уравнение линии к виду, напоминающему каноническое уравнение прямой  , найдем точку
, найдем точку 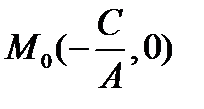 и направляющий вектор
и направляющий вектор 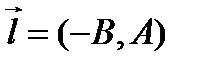 прямой, которая совпадает с данной алгебраической линией.
прямой, которая совпадает с данной алгебраической линией.
Вектор  не коллинеарен вектору
не коллинеарен вектору  (в противном случае будем иметь
(в противном случае будем иметь  ). Если система координат прямоугольная
). Если система координат прямоугольная  , то будем иметь
, то будем иметь  , то есть вектор
, то есть вектор  ортогонален направляющему вектору
ортогонален направляющему вектору  прямой, а значит, является нормальным вектором прямой.
прямой, а значит, является нормальным вектором прямой.
Таким образом, имеем геометрический смысл коэффициентов в общем уравнении прямой:  – координаты направляющего вектора, а если система координат прямоугольная, то
– координаты направляющего вектора, а если система координат прямоугольная, то  – координаты нормального вектора прямой.
– координаты нормального вектора прямой.
 2015-10-22
2015-10-22 755
755








