Вариационные принципы

Вариационныепринципы представляют собой весьма общие утверждения о рассматриваемом объекте (системе, явлении) и гласят: из всех возможных вариантов поведения (движения, эволюции) объекта выбираются лишь те, которые удовлетворяют определенному условию. Обычно согласно этому условию некоторая связанная с объектом величина достигает экстремального значения при его переходе из одного состояния в другое. Проиллюстрируем понятие вариационныхпринципов на простых примерах.

Задача №6. Автомобиль, движущийся с постоянной скоростью v, должен попасть из точки А в точку B и при этом коснуться некоторой прямой линии С. Водитель автомобиля очень торопится и выбирает из множества траекторий путь, требующий минимальных затрат времени. Найти условие минимальных временных затрат.

Рис.4

Решение. Представим затраченное время как функцию величины α – угла между прямой и отрезком пути от точки А до прямой (см. рис.4).

Время, затраченное на путь S при скорости v, вычисляется по формуле t (α) = 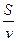, где

S = АС+ВС = , тогда t (α) =

Условие экстремальности t (α) по аргументу α означает, что или

. (12)

Для любых значений α справедливо равенство

c = ,

где с – расстояние между проекциями точек А и В, одинаковое для всех траекторий, дифференцируя его, получаем

b ,

тогда имеем

, (13)

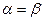и, подставляя полученное соотношение в условие минимальности (9), находим . Таким образом, получаем и, следовательно, , то есть условие минимальности привело к выбору такой траектории движения, что «угол падения равен углу отражения». Этому же закону подчиняется и ход светового луча, падающего на отражающую поверхность, что обеспечивает быстрейшее попадание сигнала из одной точки в другую (известный вариационный принцип Ферма).

Задача №7. Получить закон преломления лучей на границе двух сред, учитывая, что скорость движения света в первой среде , а во второй среде .

Решение. Если α – угол падения, а – угол его преломления, то время прохождения луча t (α) из точки А в точку В (см. рис.5) вычисляется по формуле t (α) =

Рис. 5.

Условие минимальности t (α) записывается в виде или

,

а, с учетом (13), приходим к равенству

, (14)

то есть к известному закону преломления света.

Упражнение 3. Показать, чтоводитель автомобиля, следующий принципу «минимального времени» и желающий попасть из точки А, находящейся на песчаной почве (скорость движения v₁), в точку В, расположенную на травяном лугу (скорость движения v₂), обязан поехать не по прямой линии, соединяющей точки А и В, а по ломаной траектории. Найти эту траекторию.

Универсальность вариационных принципов выражается в том, что, сформулированные для определенного класса явлений, они позволяют единообразно строить математические модели.

Дадим общую схему вариационного принципа Гамильтона для механической системы. Пусть имеется механическая система, все взаимодействия между элементами которой определяются законами механики. Введем понятие обобщенных координат Q (t), полностью определяющих положение механической системы в пространстве. Величину естественно назвать обобщенной скоростью механической системы в момент времени t. Набор величин Q (t) и определяет состояние механической системы во все моменты времени.

Для описания механической системы вводится функция Лагранжа, которая, как правило, имеет ясный смысл и записывается в виде

,

где – кинетическая и потенциальная энергия системы соответственно. Далее введем величину 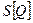, называемую действием:

.

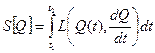Принцип Гамильтона – принцип наименьшего действия для механической системы гласит: если система движется по законам механики, то Q(t) – стационарная функция для 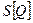или , здесь φ(t) – некоторая пробная функция, такая, что φ(t ₁) = φ(t ₂)=0 и Q (t) + εφ(t) – возможная координата данной системы. Функция εφ(t) называется вариацией величины Q (t).

Смысл принципа Гамильтона в том, что из всех мыслимых (допускаемых) траекторий системы между моментами времени реализуется движение, доставляющее минимум функционалу действия.

Итак, схема применения принципа Гамильтона состоит в том, что определяются обобщенные координаты Q (t) и обобщенные скорости системы, строятся функция Лагранжа и функционал действия 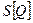, минимизация которого и дает искомую модель.

Воспользуемся принципом Гамильтона для построения модели движения шарика, соединенного с пружиной.

Задача №8. С помощью принципа Гамильтона найти уравнение движения шарика, присоединенного к пружине с жестко закрепленным концом, пренебрегая трением и сопротивлением воздуха.

Решение. В качестве обобщенной координаты системы естественно выбрать обычную эйлерову координату шарика Q (t)= , тогда обобщенная скорость – обычная скорость шарика. Функция Лагранжа записывается в виде

,

так как потенциальная энергия получается из закона Гука и равна

Для величины действия получаем выражение

.

Вычислим действие на вариациях εφ(t) координаты :

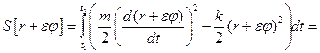
дифференцируя его по ε, полагая ε=0, получаем

.

Интегрируем первый член в скобках по частям и, учитывая что φ(t ₁)= φ(t ₂)=0, приходим к следующему уравнению

,

которое в силу произвольности функции , может удовлетворяться лишь в случае

. (15)

Таким образом, получено уравнение колебания шарика на пружине.

Упражнение 4. Получить уравнение (12) колебания шарика на пружине используя закон Ньютона (способ 1) и используя закон сохранения энергии (способ 2).

Приведем еще один пример применения принципа Гамильтона с подробным описанием механической системы

Задача №9. На неподвижном шарнире подвешен маятник – груз массы m, находящийся на конце стержня длины l. Написать уравнение колебаний маятника.

Решение. Шарнир читается идеально гладким и неподвижным, стержень считается невесомым и абсолютно жестким, груз имеет небольшие размеры по сравнению с длиной стержня, ускорение свободного падения g постоянно, сопротивлением воздуха пренебрегаем. После всех этих предположений ясно, что положение маятника определяется одной обобщающей координатой – углом отклонения стержня от вертикали Q (t)= α (t), обобщенная скорость в данном случае – угловая скорость .

Кинетическая и потенциальная энергии задаются формулами:

,

,

где h – отклонение маятника от наинизшего положения по вертикали, тогда функция Лагранжа и действие имеют вид:

,

.

Здесь мы опустили член mgl так как потенциальная энергия определяется с точностью до постоянной.

Находя действие на вариациях

и дифференцируя его по ε, полагая ε=0, получаем

.

Интегрируем первый член в интеграле по частям и, учитывая что φ(t ₁)= φ(t ₂)=0, приходим к следующему уравнению

,

которое в силу произвольности , может удовлетворяться лишь в случае

, (16)

таким образом, получено уравнение колебания маятника. Заметим, что это уравнение нелинейно. Если угол α мал, а значит sinα≈ α, то имеем линейную модель малых колебаний маятника в виде

(17)

Приведенные примеры использования принципа Гамильтона иллюстрируют весьма четкую программу действий. Универсальность, строго формализованная последовательность действий делают вариационные принципы весьма привлекательными, а иногда и единственно возможными методами.