Жесткие» и «мягкие» математические модели

Простейшим примером «жесткой» модели является таблица умножения. Простейший пример «мягкой» модели – «чем дальше в лес, тем больше дров». В случае математических моделей примером «жесткой» модели является модель Мальтуса изменения численности популяций, имеющая вид:

, где k – константа.

Эта жесткая модель описывает не только изменение численности популяций, но применима, например, к развитию науки в 1700 – 1950 годах (измеряемому, скажем, числом научных статей). При k > 0 она дает экспоненциальный рост изучаемой величины. Продолжение экспоненциального роста в дальнейшем быстро привело бы к исчерпыванию ресурсов. Ясно, что общество не может это допустить и, следовательно, развитие науки должно быть подавлено. Аналогичные явления насыщения происходят в любой популяции: когда население становится слишком большим, мальтусовская жесткая модель с постоянным коэффициентом роста k перестает быть применимой и должна быть заменена на мягкую модель

. (21)

Простейшим примером является выбор , что приводит к логистической модели вида

. (22)

Как только фиксируем a и b,логистическая модель становиться жесткой, но выводы, которые справедливы для нее, остаются справедливыми для широкого класса моделей с убывающими по N функциями k (N). Когда население мало , она очень близка к мальтусовской модели, но при достаточно больших N наблюдается резкое отличие от мальтусовского роста: вместо ухода на бесконечность, население приближается к стационарному значению. Логистическая модель удовлетворительно описывает многочисленные явления насыщения, в частности, является обычной в экологии.

Анализ размерностей

Одно из фундаментальных свойств природных, технологических, экономических и многих других объектов – симметрия (подобие, повторяемость, воспроизводимость). Типичный подход к использованию свойств симметрии – анализ размерностей величин, входящих в модель. Анализируя размерности величин, участвующих в процессе, можно найти зависимости между этими величинами и смоделировать изучаемый процесс. Прежде, чем это показать, дадим необходимые определения.

Опр.1. Система единиц измерения – совокупность основных единиц измерения, достаточных для измерения характеристик рассматриваемого класса явления.

Опр.2. Классом систем единиц измерения называется совокупность систем единиц измерения, отличающаяся между собой только величиной основных единиц измерения.

Опр.3. Размерностью физической величины называется функция, определяющая во сколько раз изменится численное значение этой величины при переходе от исходной системы единиц измерения к другой системе внутри одного класса.

Опр.4. Величины, численные значения которых остаются одинаковыми внутри данного класса, называются безразмерными, а все остальные размерными.

Утверждение1. Внутри данного класса все системы единиц измерения равноправны,

Утверждение2. С вязь между величинами, характеризующими объект, не должна меняться при переходе от одной системы единиц измерения к другой.

Сформулируем основную теорему, на которую опирается вся теория размерностей.

П-теорема. Пусть имеется некоторая функциональная связь

, (23)

между размерными величинами , где величины имеют независимую размерность, и пусть эта связь не зависит от выбора системы единиц измерения (инвариантна относительно выбора систем единиц измерения.). Тогда эта связь может быть записана в виде

П = F(1,...1, П₁,..П _n _- _k), (24)

то есть в виде соотношения величинами П,П₁,...,П _n _- _k, представляющими собой безразмерные комбинации из размерных величин следующего вида:

П= , П₁= ,…, П _n _- _k =

(эти величины называются П -комплексами), а показатели степеней в них те же, что и в соответствующих формулах размерностей для размерно зависимых величин , например для .

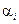Доказательство: Доказательство теоремы основано на инвариантности связи (23) относительно единиц измерения. Прежде всего, проведем обезразмеривание этого соотношения. Для каждой величины , i =1,…, k выделим безразмерный числовой коэффициент – числовое значение величины , и сомножитель , имеющий размерность и характеризующий масштаб измерения, тогда , для i =1,…, k. Числовые значения безразмерных множителей для размерно зависимых величин вычисляются с использованием масштабных множителей 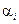, i =1,…, k по правилу

, , …, , (25)

непосредственно следующему из формул размерностей для каждой из них.

Соотношение , по предположению теоремы, не зависит от выбора системы единиц измерения, потому оно справедливо и для , ,…, – числовых значений величин , таким образом, имеем

(26)

выберем α _1,α₂,.. α _к так, чтобы α ₁= а ₁, α ₂= а ₂…, α _к= а _к, тогда (26) будет иметь вид:

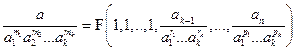(27)

и мы имеем П = F (1,...1, П₁,..П _n _- _k). Теорема доказана.

Применение П – теоремы снижает число величин, фигурирующих в описании объекта и дает способ представления искомой величины a в виде

(28)

В частности, если , то, как следует из (28),

то есть для решения получается простое выражение через задаваемые параметры и, чтобы знать точное значение a, требуется только определить константу. Приведем примеры использования этой теоремы.

Пример 1. Определить период малых колебаний маятника (см. задачу №8).

Заметим, что период малых колебаний маятника T не зависит от начального отклонения и скорости, а определяется лишь его длиной l, массой m и ускорением свободного падения g, функциональная связь содержит четыре размерные величины, три из которых имеют независимые размерности. Выберем в качестве таковых T, l, m, где , тогда для размерности g будем иметь или , откуда , что с точностью до безразмерного множителя совпадает с известной формулой для вычисления периода малых колебаний маятника. Попутно мы выяснили, что период не зависит от m.

Пример 2. Определить перепад давления на концах трубки с жидкостью.

Пусть Р – перепад давления на концах трубки. Он зависит от t, V, ρ, μ, имеющих размерности [ t ] = T, [ V ] = L ³, [ P ] = , , [ρ] = , тогда [ρ] = [μ][t][V]^-2/3, таким образом, , а так как , то имеем П= или =f(1,1,1, ), следовательно, P = ).

Пример 3. Вычислить энергию, выделяющуюся при атомном взрыве.

Предположения: при атомном взрыве в достаточно малой области (можно ее считать точкой) быстро (мгновенно) выделяется значительная энергия Е. От центра взрыва распространяется мощная ударная волна, давление за которой вначале составляет сотни тысяч атмосфер. Давлением воздуха можно пренебречь. Так, радиус фронта ударной волны есть функция: , где ρ₀ – плотность воздуха. Заметим, что размерности [ E ] = , [ t ] = T, [ ρ ₀] = – независимые, П – комплексов нет, размерность [ r ] = L удовлетворяет формуле и, следовательно, , здесь const ≈1.

Подобные явления

Определение. Явления называются подобными, если они отличаются только численными значениями определяющих их параметров, причем так, что для них соответствующие безразмерные величины П₁,П₂,…П_n-_k (параметры подобия) совпадают.

Пусть есть два явления: натуральное и модельное, при этом есть функциональная зависимость а = f (а ₁,.., а_k, а_k ₊₁,.. а_n), где а ₁,.., а_k – независимые, тогда, если a ⁽^p) = f () – реальные величины, а a ⁽^m) = f () – модельные величины, то, согласно П - теореме, имеем П⁽^p) = Ф() и П⁽^m) = =Ф(), то есть

и ,

так как П⁽^p) = П⁽^m), то возникает формула пересчета, связывающая реальные и модельные величины, а именно:

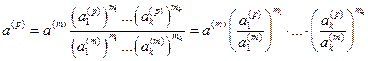Пример 1. Тело модели и тело реального предмета, находящегося в вязкой несжимаемой жидкости, отличаются только размерами. Как будут различаться их скорости?

Рассмотрим определяющие параметры: l – диаметр тела, υ – скорость тела, μ – вязкость жидкости, ρ – плотность жидкости. Они имеют размерности: [ l ] = L, , , , три из них независимы, тогда , таким образом получаем П – комплекс: , имеющий свое собственное имя: – число Рейнольдца. Так как П – комплексы одинаковы для всех единиц измерения, то получаем соотношение

или ,

которое означает, что размеры модели и объекта обратно пропорциональны их скоростям.

Пример 2. Рассмотрим движение вязкой жидкости в трубе. Как зависит скорость движения вязкой жидкости в трубе от диаметра трубы? Найти силу сопротивления среды. (Изучается поведение модели и реального объекта).

Рассмотрим определяющие параметры: l – диаметр трубы, υ – скорость движения жидкости, μ – вязкость жидкости, ρ – плотность жидкости. Как и в предыдущей задаче получаем П – комплекс (число Рейнольдца) и связь между размерами и скоростями: . Для силы сопротивления среды имеется функциональная связь F = f (l, v, μ, ρ), размерность которой выражается формулой , таким образом, , согласно П–теореме, имеем , то есть или F = μvl . Если число Re будет постоянным, то сила сопротивления будет прямо пропорциональна μvl.

В реальных условиях: F ⁽^p)= μ l ⁽^p) v ⁽^p) Ф (Re) и F ^(м)= μ l ^(м) v ^(м) Ф (Re), то есть .

Пример 3. Как меняется перепад давления, приходящийся на единицу длины при движения вязкой жидкости в трубе.

Рассмотрим определяющие параметры: l – диаметр трубы, υ – скорость движения жидкости, μ – вязкость жидкости, ρ – плотность жидкости.

Как и в предыдущих задачах получаем (число Рейнольдца) и связь для перепада давления в трубе имеет вид , для размерности имеем , следовательно, есть П – комплекс , согласно П–теореме, имеем и , таким образом,

Таким образом, перепад давления, приходящийся на единицу длины при движении вязкой жидкости в трубе прямо пропорционален скорости движения жидкости.

Пример4. Рассчитать силу сопротивления среды при движении корабля по поверхности воды, считая, что сопротивление создают только волны, возникающие при движении корабля. Вклад вязкого сопротивления считаем малым.

Рассмотрим определяющие параметры: l – размер корабля, υ – скорость движения корабля, ρ – плотность воды, g – ускорение свободного падения. Они имеют размерности: [ l ] = L, , , три из них независимы, тогда [ v ] = , таким образом получаем П – комплекс , имеющий свое собственное имя – число Фруда (Fr = ).

Для силы сопротивления среды имеется функциональная связь F = f (l, v,ρ,g), размерность которой выражается формулой , таким образом, , согласно П–теореме, имеем , то есть и , то есть сила сопротивления при движении корабля по поверхности воды прямо пропорциональна объему тела.

Выводы

1. Конструктивная математическая модель начинается со словесно-смыслового описания объекта. Эта стадия содержит сведения общего характера о природе объекта и целях его исследования.

2. Идеализация объекта. Отбрасываются все факторы и эффекты, которые представляются не самыми существенными для его поведения. По возможности идеализирующие положения записываются в математической форме.

3. Выбор или формулировка закона (вариационного принципа), которому подчиняются объекты. Его записывают в математической форме.

4. Оснащение модели. Необходимо задать сведения о начальном состоянии объекта или иные его характеристики, сформулировать цель исследования объекта.

5. Модель изучается всеми доступными способами, в том числе со взаимной проверкой различных подходов.

6..При необходимости, модель усложняется (упрощается), вводятся дополнительные факторы и исследуется новая модель.

7. В результате достигается поставленная цель и проверяется адекватность модели.

8. Желательно, чтобы сделанные выводы относились к «мягкой» модели, так как доверять выводам, сделанным на основании «жесткой» модели, можно лишь тогда, когда они подтверждаются исследованием их структурной устойчивости.

Содержание

§1. Введение. 3

§2.Элементарные математические модели. 5

§3. Принцип наибольшего благоприятствования. 9

§4. Иерархический подход к построению моделей. 11

§5. Вариационные принципы.. 20

§6. Применение аналогий при построении моделей. 27

§7. Линейность и нелинейность математических моделей. 28

§8. «Жесткие» и «мягкие» математические модели. 30

§9. Анализ размерностей. 31

§10. Подобные явления. 35

§11. Выводы: 38