Оценка справедливой стоимости и доходности акций и облигаций

Оценка справедливой стоимости акций позволяет использовать простейший алгоритм торговли на фондовом рынке: Ø если справедливая цена выше текущей цены бумаги на рынке, это стимул к приобретению такой бумаги; Ø если справедливая цена ниже текущей цены бумаги на рынке, это стимул к продаже такой ценной бумаги.
Показатель	Формула расчета
АКЦИИ
1. Доходность по акции	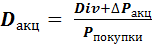, где: Div – полученные владельцем акции дивидендные выплаты; ΔP_акц– изменение курсовойстоимости акции, определяется разницей между ценой покупки и ценой продажи акции; P_{покупки} – цена приобретения акции.
2. Справедливая (рыночная) стоимость обыкновенной акции. В условиях неизменности размера дивидендов и нормы доходности можно упростить формулу на основе перпетуитета (бессрочного аннуитета). Аналогично рассчитывается и стоимость привилегированной акции.	, где: Div_t– дивиденд в t-ом периоде; r_t– норма доходности (ставка дисконтирования) в t-ом периоде; Div₀– дивиденд в первом году; r₀ – базовая, неизменная, норма доходности (ставка дисконтирования).
3. В случае предположения стабильного темпа роста дивиденда по акции и неизменности нормы доходности инвестора может использоваться формула Гордона для определения справедливой (рыночной) стоимости акции	, где: Div₁ – дивиденд в будущем году; Div₀ – дивиденд в базовом году; r – норма доходности; g – темп роста дивиденда.
ОБЛИГАЦИИ
1. Доходность по облигации	, где: D_обл– доходность облигации; K_%- Процентные (купонные) выплаты по облигации; ΔP_обл– изменение курсовой стоимости облигации, определяется разницей между ценами покупки и продажи облигации, в случае погашения облигации эмитентом цена продажи равна номиналу облигации; P_{покупки}– цена приобретения облигации.
2. Справедливая стоимость облигации	, где: K_n– купонные выплаты в n-ом периоде; N – номинал облигации.

2 3 4 5 6 7 8

Подборка статей по вашей теме: