Тригонометрическая форма комплексного числа, свойства модуля и аргумента

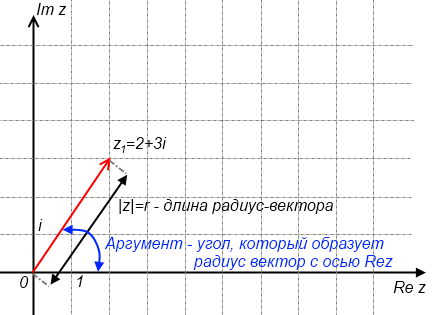
Любое комплексное число (кроме нуля) 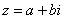можно записать в тригонометрической форме:
,

где – |z| это модуль комплексного числа (r), а 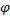– аргумент комплексного числа.

Модуль находится по т.Пифагора: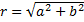

Аргумент: ,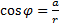

Степень комплексного числа с натуральным показателем, формула Муавра корень n-степени из комплексного числа.

формула Муавра:

Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень 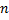справедлива формула:

Корень n-степени

Уравнение вида 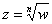имеет ровно 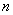корней 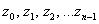, которые можно найти по формуле:
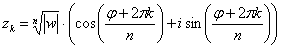, где 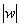– это модуль комплексного числа 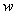, 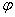– его аргумент, а параметр принимает значения:

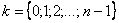
Степень числа е с комплексным показателем, формулы Эйлера, показательная форма комплексного числа.

формула Эйлера имеет вид:

С учетом тригонометрической формы комплексного числа, показательную форму можно представить в виде: