Теоремы о непрерывных функциях

Теорема 1. Если две функции и непрерывны в точке , то функции также непрерывны в точке .

Доказательство:

Так как и непрерывны в точке , то и .

Воспользуемся теоремами о пределах функции

Теорема доказана.

Теорема 2. Если функция непрерывна на отрезке , то на этом отрезке найдётся по крайней мере одна точка такая, что значение функции в этой точке будет больше, чем значение функции в любой точке этого отрезка, т.е. ; и найдётся по крайней мере одна точка такая, что значение функции в этой точке будет меньше, чем значение функции в любой точке этого отрезка, т.е. .

Значение функции называется наибольшим значением функции на отрезке, значение функции называется наименьшим значением функции на отрезке.

Теорема 3. Если функция 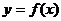непрерывна на отрезке и на концах отрезка принимает значения разных знаков, то внутри отрезка найдётся по крайней мере одна точка, в которой .

Теорема 4. Если функция 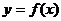непрерывна на отрезке и на концах отрезка принимает неравные между собой значения и , то каково бы ни было число внутри отрезка , такое что , найдётся по крайней мере одна точка , в которой функция принимает значение равное , т.е. .