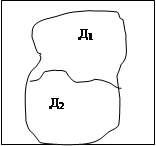
В некотором квадрате случайным образом выбирается точка, какова вероятность того, что эта точка окажется внутри области Д.
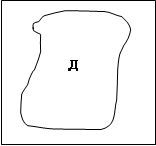 |  |
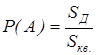 , где SД- площадь области Д, S- площадь всего квадрата.
, где SД- площадь области Д, S- площадь всего квадрата.
При классическом определенную нулевую вероятность имело только невозможное событие. Иначе обстоят дела при геометрическом определении. Действительно, рассмотрим внутри основного квадрата отрезок какой-нибудь прямой случайная точка вполне может попасть на этот отрезок, и следовательно, такое событие не является невозможным. Однако площадь отрезка равна 0, т.е. вероятность этого события, согласно геометрическому определению равна 0. Таким образом,при геометрическом определении вероятности события с нулевой вероятностью могут осуществляться.
Замечание:
1) Пусть отрезок l составная часть отрезка z. На отрезок z наудачу поставлена точка. Предполагая, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка z, определяют вероятность попадания точки на отрезок l по равенству.
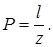
Пример: Электрический провод, соединяющий пункты A и B, порвался в неизвестном месте. Чему равна вероятность того, что разрыв произошел не далее 500м от пункта A, если расстояние между пунктами 2 км?
Решение:
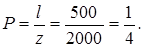
2)Аналогично определяется вероятность попадания точки в пространственную фигуру n, которая составляет часть фигуры V:
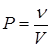 .
.
Алгебра событий.
Объединением или суммой нескольких случайных событий называется событие, состоящее в появлении хотя бы одного их данных событий.
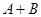
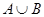
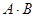
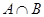
Свойства суммы и произведения событий:
1. Переместительность (коммутативность).
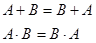
2. Сочетательность (ассоциативность).
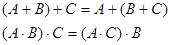
3. Распределительность (дистрибутивность).
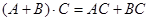
4. Идемпотентность
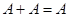
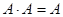
 2014-01-25
2014-01-25 1220
1220