Общие сведения
При обработке деталей на металлообрабатывающих станках применяют два принципиально разных способа получения заданных размеров:
1. Способ индивидуального получения размеров (называемый иногда способом пробных проходов и промеров) – при котором рабочий обрабатывает небольшой участок поверхности, измеряет полученный размер, рассчитывает требуемую коррекцию положения инструмента, затем, пользуясь механизмом ручной подачи, перемещает инструмент в нужном направлении и снова обрабатывает этот участок, измеряет и так далее до тех пор, пока не получит требуемый размер. После этого производится обработка всей поверхности заготовки. Работа по этому способу требует высокой квалификации рабочего-станочника.
2. Способ автоматического получения размеров, при котором обработка производится на предварительно настроенном оборудовании на заданный размер. По этому способу производится обработка деталей на станках - автоматах и полуавтоматах, копировальных станках, станках с числовым программным управлением, агрегатных станках и т.д. По этому способу автоматически получаются диаметры отверстий при обработке мерным режущим инструментом (сверлами, зенкерами, развёртками, протяжками, прошивками и т.д.), профили поверхностей при обработке фасонным и профильным инструментом (метчиками, плашками, фасонными резцами и т.д.). Преимущества этого способа очевидны: не требуется высокой квалификации рабочих, возможна обработка поверхностей любой сложности и их сочетаний и сопряжений, увеличивается производительность труда и уменьшается вероятность появления брака.
Недостатком способа автоматического получения размеров является большее, по сравнению с первым способом, количество причин, приводящих к уменьшению точности обработки.
В этой работе анализируется точность деталей, изготовленных по способу автоматического получения размеров.
Основные понятия и определения
Точность изготовления изделия – степень соответствия (приближения) изготовленного изделия заранее установленному образцу.
Точность обработки детали – степень соответствия (приближения) действительных геометрических параметров обработанной детали заданным.
Погрешность обработки – значение несоответствия действительных геометрических параметров детали заданным (количественная оценка точности).
Заданная (требуемая) точность – это точность, регламентируемая
конструктором в рабочей конструкторской документации путём назначения допусков на параметры всего изделия, сборочной единицы или отдельной детали.
Действительная точность – это точность получения параметров каждого изготовленного изделия, которая характеризуется погрешностью, определяемой сравнением действительных (объективно существующих) значений параметров заданным.
Измеренная точность – это точность познания действительного значения с использованием средств измерения, которая характеризуется погрешностью измерения, определяемой сравнением действительного и измеренного значений параметров.
Ожидаемая точность – это точность, которую предполагает получить
технолог при проектировании всего технологического процесса или отдельной операции. Она характеризуется расчётным значением погрешности, которую мы ожидаем получить после изготовления изделия.
Партия – детали, запускаемые в обработку одновременно и обрабатываемые на одном станке при одной его наладке одним инструментом до его смены или перезаточки.
Генеральная (складская) совокупность объединяет детали многих
партий, обработанных на разных станках, при разных наладках, в разное
время.
Выборка – детали, извлекаемые по определённой методике из партии или генеральной совокупности для статистических исследований точности или качества обработки.
Поле рассеивания ω – это разность наибольшего Aд max и наименьшего Ад min действительного размеров детали в пределах анализируемой совокупности:
ω = Aд max – Aд min (1)
Коэффициент точности – это соотношение между полем рассеивания и допуском:
Kт = ω/T. (2)
Нормативные значения:
0,3 < Кт < 0,5 – при обработке на оборудовании и использовании оснастки, которые по точности значительно превышают необходимую (повышенный запас точности);
0,5 < Kт < 0,75 – при обработке на оборудовании и использовании оснастки с нормальным запасом точности;
0,75 < Kт < 0,95 – при обработке на оборудовании и использовании оснастки с малым запасом точности;
0,95 < Kт < 1,05 – при обработке на оборудовании и использовании оснастки с отсутствием запаса точности и экономически оправданном небольшом уровне брака.
Классификация и законы распределения погрешностей.
В процессе выполнения операции механической обработки на точность получения каждого параметра действует одновременно множество причин, вызывающих появление первичных (элементарных) погрешностей. Эти причины различаются по характеру действия на протяжении обработки партии заготовок. Одна группа причин действует постоянно и приводит к появлению на обрабатываемых заготовках одинаковых погрешностей. При действии второй группы причин размеры обрабатываемых заготовок получаются переменными, но всегда известен закон, по которому происходит это изменение. Третья группа причин вызывает появление погрешностей, величина или знак которых заранее не известны, как неизвестен и закон, по которому произойдёт изменение этой погрешности на следующей обрабатываемой заготовке. Поэтому по характеру проявления погрешности во времени их классифицируют на систематически-постоянные, закономерно-изменяющиеся и случайные.
Систематически-постоянными называют погрешности, значение и знак которых неизменны для всех заготовок одной или нескольких партий.
К подобным погрешностям, например, относятся:
· геометрическая погрешность станка (для деталей, изготовленных только на этом станке);
· погрешность размерного и профильного инструмента (для деталей, обработанных этим инструментом);
· погрешность настройки станка на размер (для деталей, обработанных при данной настройке станка).
В пределах генеральной совокупности эти погрешности не будут постоянными.
Закономерно-изменяющейся называется погрешность, значение или знак которой изменяются при переходе от одной обрабатываемой заготовки к другой по определённому, заранее известному закону. Типичным примером подобной погрешности является погрешность, вызываемая размерным износом режущего инструмента: при обработке коротких валиков средний размер каждого последующего валика будет отличаться от предыдущего на одну и ту же величину – износ инструмента за время обработки одной детали.
Погрешность, величина которой не постоянна и меняется без видимой закономерности, называется случайной.
Операционная погрешность является результатом суммирования,
наложения этих первичных погрешностей и у годных деталей должна находиться в пределах поля допуска данного параметра.
Для анализа точности процесса необходимо иметь сведения не только о границах, в которых изменяются размеры, но также и о характере распределения размеров внутри этих границ. Характер распределения параметров показывает, располагаются ли они равномерно внутри поля рассеивания или же группируются каким-то образом около некоторого размера – центра группирования.
Рассеивание размеров партии деталей может быть близким к какому либо теоретическому закону распределения, известному из теории вероятностей. Тогда уравнение этого закона позволит оценить и поле рассеивания размеров, и характер их распределения у деталей, подлежащих обработке.
При механической обработке деталей на станках, настроенных на размер, рассеивание размеров обработки часто описывается законом нормального распределения (рис. 1, а), законом равной вероятности (рис. 1, б) или законом распределения, являющимся композицией двух первых (рис 1, в).
Закон нормального распределения (закон Гаусса) имеет место тогда,
когда причины, порождающие рассеивание параметров, многочисленны, являются случайными, и среди них нет доминирующих.

Рис.1 Законы распределения погрешностей а – закон нормального распределения; б – закон равной вероятности; в – композиционный закон.
Закон равной вероятности, наоборот, имеет место при наличии погрешности, изменяющейся во времени по линейному закону (закономерно - изменяющаяся погрешность). Концепция законов нормального распределения и равной вероятности является результатом случайных и закономерно изменяющихся факторов. Основными характеристиками законов распределения являются мате магическое ожидание (среднее арифметическое значение параметра) M(Dx) и среднее квадратическое отклонение s. Они при дискретных значениях размера определяются по следующим соотношениям:
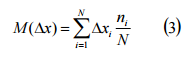

Плотность вероятности нормального закона распределения описывается следующей формулой:

Если изменение случайной величины следует закону нормального распределения, то она может принимать любые значения в пределах ± ¥. При этом можно считать, что практически все детали партии имеют размеры, находящиеся в пределах ±3s, отсчитываемых от среднего значения (мат.ожидания). В этих пределах под кривой нормального распределения заключено 99,73% всей ее площади. Поэтому теоретическое поле рассеивания w ограничено 6s. Размерность среднего квадратичного отклонения совпадает с размерностью самой случайной величины. Теоретическое поле рассеивания позволяет дать оценку метода обработки, прогнозировать точность обработки сколько угодно большого числа деталей. Для того чтобы все детали были годными необходимо соблюдение двух условий:
1. Поле рассеивания случайной величины должно быть равно или меньше допуска размера выдерживаемого при обработке: w £ Т.
2. Поле рассеивания размеров w должно располагаться в границах поля допуска Т. Несоблюдение одного из этих условий приводит к появлению бракованных деталей. Вместо размеров деталей можно в равной степени оперировать отклонениями размеров. Отклонения размеров, равно как и сами размеры обработанных деталей есть случайные геометрические параметры. В основе статистического метода определения суммарной погрешности лежат законы и правила теории вероятностей и математической статистики. Статистический метод анализа точности процессов включает в себя:
· измерение обработанных деталей;
· статистическую обработку результатов измерений и расчет основных точностных характеристик процесса обработки;
· сравнение поля допуска и поля рассеивания контролируемого размера;
· определение путей улучшения процесса обработки.
Наличие случайных и закономерно-изменяющихся погрешностей приводят к рассеиванию размеров обрабатываемых деталей. Рассеивание геометрических параметров определяет точность обработки партии деталей.
Знание характера распределения размеров необходимо:
· для анализа причин, вызывающих рассеивание размеров;
· для определения суммарного влияния погрешностей при обработке;
· для оценки качества настройки системы СПИД;
· для количественного определения вероятности получения бракованных деталей.
Лабораторная работа № 6
Статистические методы исследования точности
Цель работы:
Задание:
1. Провести статистическую обработку результатов измерения диаметров партии деталей, обработанных на бесцентрово-шлифовальном станке, настроенном на размер.
2. Основываясь на полученных данных, дать рекомендации по настройке станка.
 2020-06-12
2020-06-12 948
948







