Интегрирование по частям

Из формулы дифференциала произведения  почленным интегрированием и получается формула интегрирования по частям:

.

Эта формула применяется тогда, когда под знаком интеграла стоит произведение алгебраической и трансцендентной функций. Например, , ,  и др. При этом за «u» выбирают функцию, которая при дифференцировании упрощается, а за dv – ту часть подынтегрального выражения, интеграл от которой легко найти.

○ Пример 1. Найти интеграл

Решение.

.

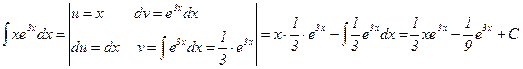○ Пример 2. Найти интеграл

Решение.

.

○ Пример 3. Найти интеграл .

Решение.

Рассмотрим способы интегрирования наиболее часто встречающихся функций.