Свойства уравнений Максвелла

Глава 7. Электромагнитное поле

Уравнения Максвелла

 

В 1865 году Максвелл, основываясь на идеях Фарадея об электрическом и магнитном полях, обобщил законы, установленные экспериментальным путем, и разработал законченную теорию единого электромагнитного поля, создаваемого произвольной системой зарядов и токов.

Теория Максвелла представляет собой феноменологическую теорию электромагнитного поля. Это означает, что внутренний механизм явлений, происходящих в среде и вызывающих появление электрических и магнитных полей, в теории не рассматривается.

Теория Максвелла является макроскопической теорией электромагнитного поля, создаваемого макроскопическими зарядами и токами.

Электромагнитное поле – совокупность двух взаимосвязанных полей – электрического и магнитного.

Электромагнитное поле описывают следующими векторами:

 (напряжённость электрического поля);

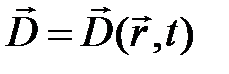 (электрическая индукция (электрическое смещение));

 (магнитная индукция);

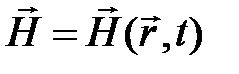 (напряжённость магнитного поля).

Уравнения Максвелла содержат 4 уравнения в интегральной форме, 4 уравнения в дифференциальной форме и 3 уравнения связи (материальные уравнения).

Уравнения Максвелла нельзя строго вывести или доказать, поэтому они являются обобщениями уже известных законов.

Запишем уравнения Максвелла в интегральной форме.

Первое уравнение.

Первое уравнение Максвелла является обобщением закона электромагнитной индукции Фарадея для .

Как было показано в 6.2,  

                                        .

Магнитный поток .

Считая поверхность интегрирования  - неподвижной и, учтя, что , получим

     .

Тогда первое уравнение Максвелла можно записать в виде

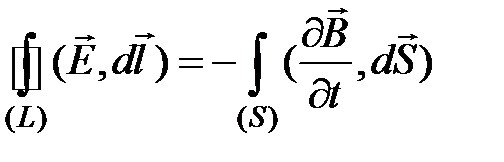        ,             (7.1)

где любой замкнутый контур, мысленно выбранный в переменном магнитном поле; поверхность, ограниченная контуром 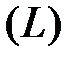; переменное во времени магнитное поле.

Из уравнения (7.1) можно сделать вывод: изменяющееся во времени магнитное поле порождает вихревое электрическое поле.

 

Второе уравнение:

Второе уравнение является обобщением закона полного тока.

Максвелл предположил, что переменное электрическое поле, также как электрический ток, является источником магнитного поля. Он ввел новое понятие  ток смещения, следующим образом:

По теореме Гаусса для вектора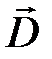

,

где 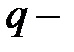 сторонние заряды.

Продифференцируем это выражение по времени

.

С учетом, что , и считая поверхность интегрирования неподвижной

.

Правая часть этого уравнения имеет размерность силы тока, тогда и левая часть должна ее иметь.

Используя формулу , Максвелл предположил, что  имеет размерность плотности тока. Поэтому он предложил назвать   плотностью тока смещения:

.

Тогда                  .

Введя представление о токе смещения, Максвелл поменял имеющиеся на тот момент представления о цепях переменного тока. Цепи постоянного тока должны быть замкнутыми, но для цепей переменного тока это условие считалось необязательным. Предполагалось, что при зарядке и разрядке конденсатора электрический ток проходит по проводнику, соединяющему обкладки конденсатора, и не проходит через диэлектрик, находящийся между обкладками, т.е. цепь не замкнута. Максвелл же доказал, что ток смещения как раз и проходит через диэлектрик, обеспечивая замкнутость таких цепей. Таким образом, линии переменного тока всюду замкнуты, также, как и линии постоянного тока.

В общем случае ток проводимости и ток смещения не разделены в пространстве. Все типы токов существуют в одном и том же объеме и тогда можно говорить о полном токе, равном сумме тока проводимости и тока смещения.

.

где  – плотность тока проводимости; сила тока проводимости.

Обобщив для 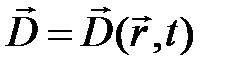 и, используя теорему о циркуляции  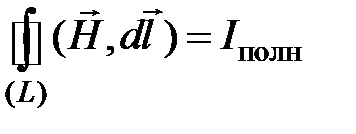Максвелл получил второе уравнение:

       .               (7.2)

Из уравнения (7.2) можно сделать вывод: ток проводимости и, изменяющееся во времени электрическое поле, порождают магнитное поле.

Третье уравнение.

Третье уравнение Максвелла обобщает теорему Гаусса для поля вектора  

.                         (7.3)

Из (7.3) можно сделать вывод: источником вектора электрического смещения  являются сторонние заряды.

 

Четвёртое уравнение.

Четвертое уравнение обобщает теорему Гаусса для поля вектора магнитной индукции :

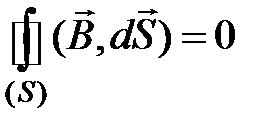                                                                    (7.4)

Из (7.4) можно сделать вывод: в природе отсутствуют однополюсные магнитные заряды (монополи).

 

 Используя теоремы Стокса и Остроградского-Гаусса, из уравнений Максвелла в интегральной форме можно перейти к уравнениям Максвелла в дифференциальной форме, которые более удобны для описания электромагнитного поля:

                                                              (1)           

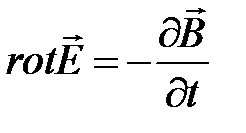
                                                              (2)                                               (7.5)                                                                           

                                                              (3)            

                                                              (4)               

                               

Систему уравнений Максвелла необходимо дополнить материальными уравнениями, характеризующими электрические и магнитные свойства среды.

Для изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков

                             (7.6)

где  – удельная электрическая проводимость; – диэлектрическая проницаемость среды; – магнитная проницаемость среды; напряженность поля сторонних сил.

Представим уравнения (1)-(4) через оператор :

                                                            (1)            ;

                                                             (2)            ;                              (7.7)                        

                                                             (3)             ;

                                                              (4)              .

Уравнения Максвелла в дифференциальной форме с уравнением движения заряженных частиц под действием силы Лоренца , составляют фундаментальную систему уравнений, которая, в принципе достаточна, для описания всех электромагнитных явлений, в которых не проявляются квантовые эффекты.

Дальнейшим развитием теории электромагнитного поля Максвелла явилась электронная теория, созданная Лоренцем.

 

 

Свойства уравнений Максвелла

1. Уравнения Максвелла – линейны (содержат первые производные векторов  и первые степени . Свойство линейности связано с принципом суперпозиции полей.

 

2. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда .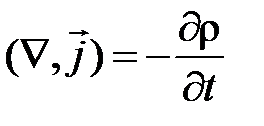

      Покажем это. Запишем 2 уравнение Максвелла через оператор .

         . Возьмем от левой и правой частей уравнения:

          . Учитывая, что , получим

 

.

 

3. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя  в них преобразуются по определенным правилам.

 

4. Уравнения Максвелла не симметричны относительно электрических и магнитных полей (существуют электрические заряды, но нет магнитных зарядов). Для нейтральной однородной непроводящей среды , они симметричны (за исключением знака).

 

                                             (левовинтовая система),

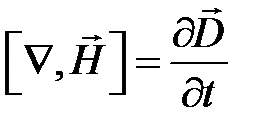                                                   (правовинтовая система).

 

5. Из уравнений Максвелла вытекает существования электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью.