2014-02-24
21804
Введение тока смещения позволило Максвеллу блестяще завершить единую теорию электромагнитного поля. Эта теория не только позволила объяснить все разрозненные явления электричества и магнетизма, но и предсказала ряд новых явлений, которые были подтверждены впоследствии.
Эта теория базируется на единой системе четырех уравнений Максвелла, которая может быть записана в интегральной и дифференциальной форме.
Уравнения Максвелла в интегральной форме:
1. 
;
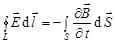2. 
;
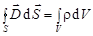3. 
;
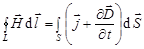4. 
.
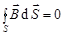Содержание этих уравнений заключается в следующем:
1. Циркуляция вектора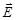 
по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под 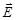понимается не только вихревое электрическое поле, но и электростатическое (циркуляция такого поля равна нулю).
2. Поток вектора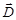 
сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. (Фактически это теорема Гаусса для поля заряда, распределенного внутри замкнутой поверхности с объемной плотностью 
)
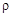3. Циркуляция вектора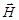 
по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
4. Поток вектора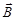 
сквозь произвольную замкнутую поверхность всегда равна нулю. Данное уравнение постулирует отсутствие в природе «магнитных» зарядов. (Это теорема Гаусса для магнитного поля)
Из уравнений Максвелла для циркуляции векторов 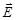и 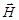следует, что электрическое и магнитное поле нельзя рассматривать как независимые: изменение во времени одного из них приводит к появлению другого. Таким образом, следует рассматривать единое электромагнитное поле.
В то же время в случае стационарных поле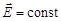й (
и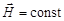 
) система уравнений Максвелла распадается на две группы независимых уравнений:
; 
;
; .
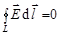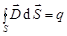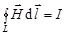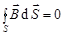В этом случае электрическое и магнитное поля независимы друг от друга, поэтому могут рассматриваться физически и математически раздельно.
