Цель: сформировать умение применять формулы сокращенного умножения для старших степеней.
Теоретические сведения к практическому занятию:
Выражение вида 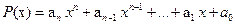 , где
, где 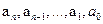 — некоторые числа и
— некоторые числа и 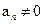 , называется многочленом степени n от х.
, называется многочленом степени n от х.
Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях х. Многочлены 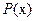 и
и  тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях этих многочленов одинаковы.
тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях этих многочленов одинаковы.
Многочлен Р(х) степени n имеет не более n корней.
Если многочлен Р(х) степени n имеет n корней (среди которых могут быть равные), то он представим в виде 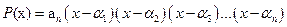

Бином Ньютона:
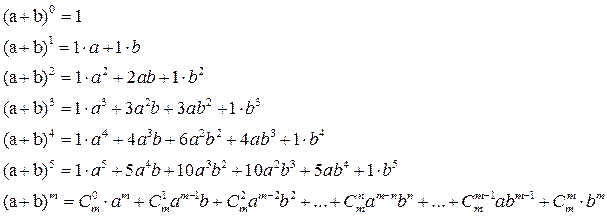
5

Самостоятельная работа:
Применить формулы сокращенного умножения:

Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение многочлена степени n. Приведите примеры.
2) Какие многочлены называются равными?
3) Укажите формулу бинома Ньютона.
4) Объясните как получить данные чисел в треугольнике Паскаля. Приведите примеры
Б. Выполнить задания:
Записать разложение бинома:

Тема: «Степень с рациональным и действительным показателем, свойства»
Цель: сформировать умение применять свойства степеней при решении различных упражнений.
Теоретические сведения к практическому занятию:
Если m – целое число, n – натуральное число,an=а∙а∙а∙а∙…∙а
а1=а
а0=1 (а≠0)
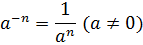
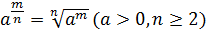
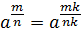
Если r>0, то 0r=0.
Примеры:

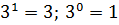
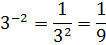

Свойства:
Пусть 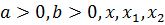 – действительные числа
– действительные числа
1) 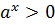
2) Если 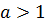 и
и  ,то
,то 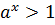
3) Если 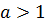 и
и 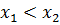 ,то
,то 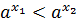
4) Если 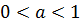 и
и 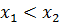 ,то
,то 
5) Если  , где
, где  ,то
,то 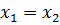
6) Если 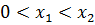 и
и  ,то
,то 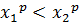
7) Если 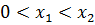 и
и 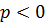 ,то
,то 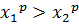
8) 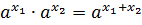
9) 
10) 
11) 
12) 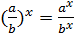
Примеры:
1) 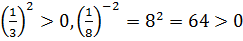
2) 
3) 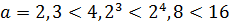
4) 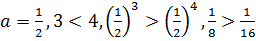
5) 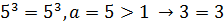
6) 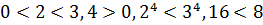 1
1
7) 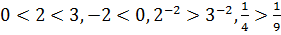
8) 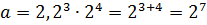 =128
=128
9) 
10) 
11) 
12) 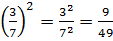
Самостоятельная работа:
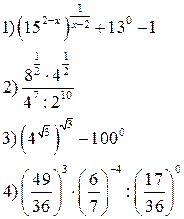
5) Записать и выучить таблицу степеней
Содержание практического занятия:
А. Ответить на вопросы:
1) Что означает операция возведения числа в нулевую степень? Приведите примеры.
2) Что означает операция возведения числа в первую степень? Приведите примеры.
3) Что означает операция возведения числа в отрицательную степень? Приведите примеры.
4) Назовите основные свойства степени. Приведите примеры.
Б. Выполнить задания:
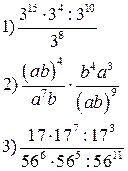
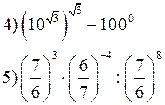
8
 2020-09-24
2020-09-24 369
369








