Основные численные методы решения дифференциальных уравнений
Семестр
Целью данной главы учебного пособия является рассмотрение основных численных методов интегрирования дифференциальных уравнений [1,2,3].
Численные методы решения дифференциальных уравнений используются в тех случаях, когда не удается найти их решение в аналитическом виде. Прежде всего, это относится к линейным дифференциальным уравнениям с переменными коэффициентами и нелинейным дифференциальным уравнениям, соответственно описывающим динамику линейных нестационарных и нелинейных систем управления.
С помощью данных методов, прежде всего, решаются задачи исследования систем.
В данной части пособия ограничимся рассмотрением методов решения только для задачи Коши.
Рассмотрим дифференциальное уравнение
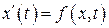 . (1.1)
. (1.1)
Предположим, что функция 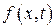 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 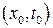 . Задача Коши для дифференциального уравнения (1.1) формулируется следующим образом: найти решение
. Задача Коши для дифференциального уравнения (1.1) формулируется следующим образом: найти решение 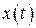 уравнения (1.1), удовлетворяющее условию
уравнения (1.1), удовлетворяющее условию 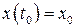 .
.
Предположим, что известно решение 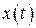 в точке
в точке 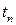 и требуется найти
и требуется найти 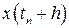 , где
, где 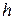 – шаг интегрирования. Согласно формуле Ньютона – Лейбница, очевидным является следующее равенство
– шаг интегрирования. Согласно формуле Ньютона – Лейбница, очевидным является следующее равенство
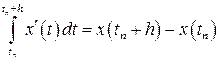 .
.
Запишем его следующим образом
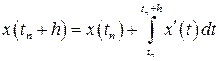 .
.
Учитывая уравнение (1.1), последнее равенство можно записать в виде
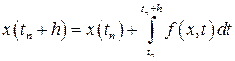 . (1.2)
. (1.2)
Интеграл в правой части выражения (1.2) приближенно можно вычислить, используя формулу прямоугольников:
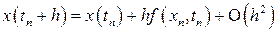 .
.
Здесь 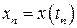 . Отбрасывая члены порядка
. Отбрасывая члены порядка 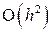 и полагая
и полагая 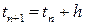 ,
, 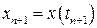 , получаем известную формулу Эйлера
, получаем известную формулу Эйлера
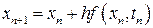 ,
, 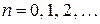 . (1.3)
. (1.3)
Аналогичный результат можно получить и другим способом. Для этого разложим функцию 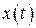 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 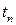 , в результате получим
, в результате получим
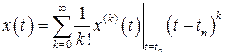 (1.4)
(1.4)
или
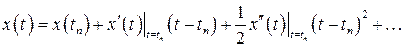 .
.
В последнем выражении ограничимся двумя первыми слагаемыми в правой части. В результате получаем
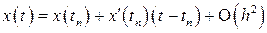 ,
, 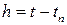 .
.
Полагаем, что решение 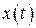 в точке
в точке 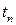 известно. Тогда решение в точке
известно. Тогда решение в точке 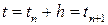 можно найти, используя последнюю формулу и учитывая, что
можно найти, используя последнюю формулу и учитывая, что 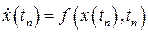 :
:
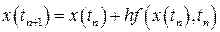 (1.
(1.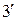 )
)
или
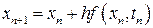 ,
, 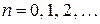 .
.
Начинать вычислительный процесс необходимо с точки, определяющей начальные условия, то есть 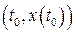 .
.
Вычислительный процесс, построенный по формуле (1.3), имеет локальную погрешность, пропорциональную 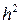 . Это означает, что на каждом шаге интегрирования имеет место погрешность порядка
. Это означает, что на каждом шаге интегрирования имеет место погрешность порядка 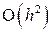 . Соответственно, при увеличении времени интегрирования общая погрешность решения дифференциального уравнения возрастает.
. Соответственно, при увеличении времени интегрирования общая погрешность решения дифференциального уравнения возрастает.
Повысить точность получаемых результатов можно, если учитывать большее количество членов разложения функции 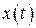 в ряд Тейлора. Однако, для этого необходимо последовательно дифференцировать правую часть дифференциального уравнения (1.1).
в ряд Тейлора. Однако, для этого необходимо последовательно дифференцировать правую часть дифференциального уравнения (1.1).
Рассмотрим это на конкретном примере.
Учтем первые четыре члена в ряде Тейлора, в результате получим
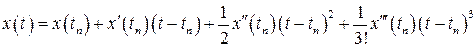 .
.
Как и ранее, полагаем, что решение в точке 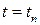 найдено. Выбирая достаточно малый шаг
найдено. Выбирая достаточно малый шаг 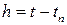 , находим решение в следующей точке
, находим решение в следующей точке 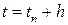
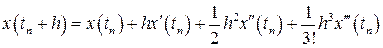 .
.
Для реализации этой формулы необходимо знать производные искомого решения 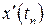 ,
, 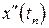 ,
, 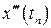 . Первая производная
. Первая производная 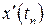 может быть найдена из дифференциального уравнения (1.1). Это есть его правая часть,
может быть найдена из дифференциального уравнения (1.1). Это есть его правая часть, 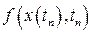 . Вторую и третью производные решения –
. Вторую и третью производные решения – 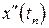 ,
, 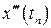 – можно найти, дифференцируя правую часть уравнения (1.1), рассматривая ее, как сложную функцию. Соответственно имеем
– можно найти, дифференцируя правую часть уравнения (1.1), рассматривая ее, как сложную функцию. Соответственно имеем
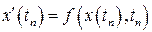 ,
,
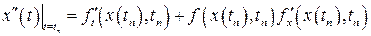 , (1.5)
, (1.5)
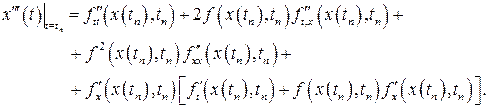
Как видим, такой путь повышения локальной точности решения дифференциального уравнения (1.1) является трудоемким.
Точность вычислений можно повысить при заданном шаге интегрирования 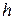 и другими способами. В формуле (1.2) интеграл вычисляется по формуле прямоугольников. Вычислим этот интеграл, используя формулу трапеций. В результате будем иметь
и другими способами. В формуле (1.2) интеграл вычисляется по формуле прямоугольников. Вычислим этот интеграл, используя формулу трапеций. В результате будем иметь
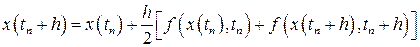 .
.
По формуле Тейлора, справедливо равенство
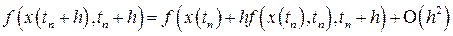 .
.
Отбрасывая в последнем выражении члены порядка 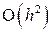 , и полагая
, и полагая
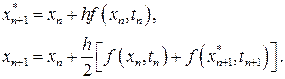 (1.6)
(1.6)
Здесь 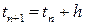 .
.
Погрешность, которая обеспечивается этими формулами, имеет порядок 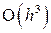 . Формулы (1.6) называются формулами Эйлера – Коши.
. Формулы (1.6) называются формулами Эйлера – Коши.
1.2. Методы Рунге – Кутта
Полагаем, что функция 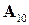 имеет непрерывные частные производные до
имеет непрерывные частные производные до 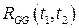 -го порядка включительно, тогда решение задачи Коши для уравнения (1.1) будет обладать непрерывными производными до
-го порядка включительно, тогда решение задачи Коши для уравнения (1.1) будет обладать непрерывными производными до 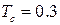 -го порядка включительно. Если значение известно в точке
-го порядка включительно. Если значение известно в точке 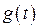 , то справедливо равенство
, то справедливо равенство
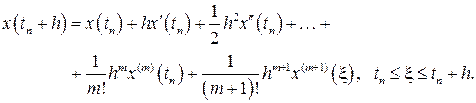 (1.7)
(1.7)
Как уже отмечалось, значения входящих в данную формулу производных вычисляются последовательным дифференцированием уравнения (1.1), что является достаточно трудоемким процессом.
Для сокращения вычислительной работы Рунге предложил искать значение 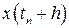 в виде
в виде
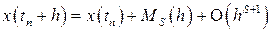 , (1.8)
, (1.8)
где
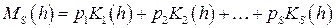 ,
,
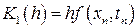 ,
,
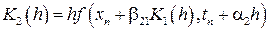 ,
,
…
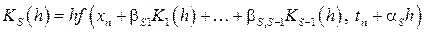 ,
,
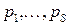 ;
; 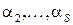 ;
; 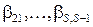 – некоторые постоянные параметры.
– некоторые постоянные параметры.
Формула Эйлера (1.3) представляет собой частный случай формулы (1.7) при 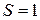 , а формулы (1.6) – при
, а формулы (1.6) – при 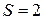 .
.
Рассмотрим вопрос о выборе параметров 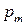 ,
, 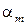 ,
, 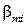 . Для простоты ограничимся случаем
. Для простоты ограничимся случаем 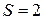 . Введем обозначения
. Введем обозначения
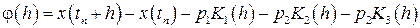 . (1.9)
. (1.9)
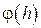 – ошибка, которая имеет место на
– ошибка, которая имеет место на 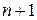 шаге интегрирования для получения
шаге интегрирования для получения 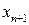 , при известном
, при известном 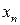 .
.
Из выражения (1.7) следует, что
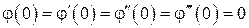 . (1.10)
. (1.10)
Учитывая соотношения (1.5), из равенства (1.9) имеем
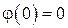 ,
,
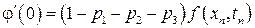 ,
,
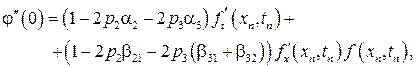
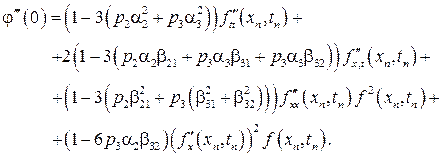
Приведенные выше условия (1.10) будут выполняться, если справедлива следующая система равенств
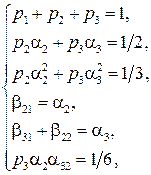
поскольку 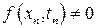 ,
, 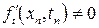 ,
, 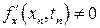 ,
, 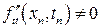 ,
, 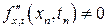 ,
, 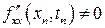 .
.
Это – система из шести уравнений с восемью неизвестными, имеющая бесконечное множество решений. Наиболее употребительное решение системы (1.16)
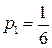 ,
, 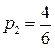 ,
, 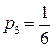 ,
,
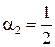 ,
, 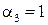 ,
,
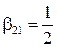 ,
, 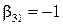 ,
, 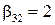 .
.
Эти решения порождают следующие расчетные формулы
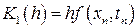 ,
,
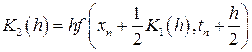 , (1.11)
, (1.11)
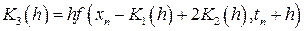 .
.
Соответственно,
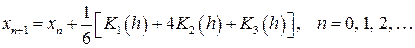 . (1.12)
. (1.12)
Вычислительная схема, реализуемая по формулам (1.11), (1.12) называется методом Рунге-Кутта 3-го порядка.
При 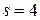 получаем наиболее распространенную вычислительную схему метода Рунге-Кутта
получаем наиболее распространенную вычислительную схему метода Рунге-Кутта
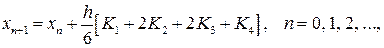 (1.13)
(1.13)
где
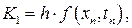
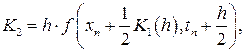
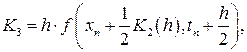
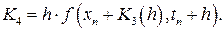
Еще раз отметим, что на каждом шаге интегрирования по методам Рунге-Кутта, согласно формуле (1.8) имеем локальную точность вычислений порядка 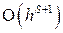 .
.
Рассмотренные методы интегрирования дифференциального уравнения являются одношаговыми. То есть для построения решения на следующем шаге необходимо знать информацию о значении решения только на предыдущем шаге.
Более быстродействующими являются многошаговые методы. Они используют информацию о поведении решения в нескольких предыдущих точках: 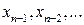 .
.
 2014-02-05
2014-02-05 3409
3409