среднего квадратического отклонения нормального распределения
1. Если 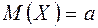 неизвестно, то доверительный интервал для оценки
неизвестно, то доверительный интервал для оценки 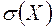 имеет вид:
имеет вид:
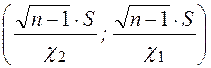
где 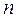 - объем выборки;
- объем выборки; 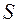 - исправленное среднее квадратическое отклонение:
- исправленное среднее квадратическое отклонение:
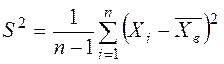 ,
,
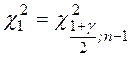 ,
, 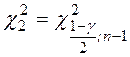 - квантили
- квантили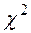 - распределения, определяемые по таблице
- распределения, определяемые по таблице 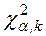 (Приложение 3)
(Приложение 3)
при 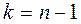 и
и 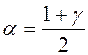 ,
, 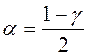 .
.
Пример 8. Для оценки параметра 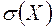 нормально распределенной случайной величины была сделана выборка объема в 25 единиц и вычислено
нормально распределенной случайной величины была сделана выборка объема в 25 единиц и вычислено 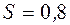 .
.
Найти доверительный интервал, покрывающий 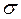 с вероятностью
с вероятностью 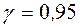 .
.
¦ Имеем 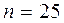 ,
, 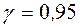 .
.
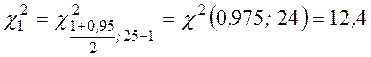
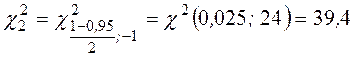
Доверительный интервал имеет вид:
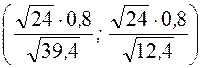 или
или 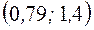 .?
.?
2. Другой вид доверительного интервала для оценки 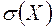 нормального распределения имеет вид:
нормального распределения имеет вид:
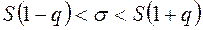 при
при 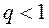 ;
;
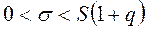 при
при 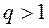 ;
;
где 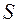 - исправленное среднее квадратическое отклонение;
- исправленное среднее квадратическое отклонение;
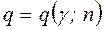 находим по таблице значений (Приложение 5).
находим по таблице значений (Приложение 5).
Пример 9. Для оценки параметра нормально распределенной случайной величины была сделана выборка объема в 25 единиц и вычислено 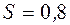 .
.
Найти доверительный интервал, покрывающий 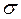 с вероятностью
с вероятностью 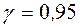 .
.
¦ Имеем 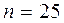 ,
, 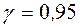 ,
, 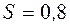
По таблице значений 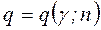 находим
находим 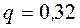 .
.
Доверительный интервал имеет вид:
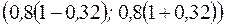 или
или 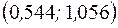 .?
.?
Замечание. Доверительные интервалы в примерах 8 и 9 получили разные при одинаковых данных, но они с вероятностью 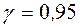 покрывают среднее квадратическое отклонение
покрывают среднее квадратическое отклонение 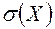 .
.
 2014-02-02
2014-02-02 1480
1480
