2014-02-17
1314
Динамические механические характеристики электропривода выражают собой зависимости координат механической части электропривода от времени, а именно М, МС, МД=f(t), а также угловой скорости от времени ω=f(t).
Представим семейства динамических характеристик для следующих примеров:
1. К единичному элементу, находящемуся в неподвижном состоянии (то есть ω=0) одновременно приложены два момента:
а) Вращающий электромагнитный момент М=f(ω);
б) Статический момент МС=f(ω).
При этом если представить зеркальное отображение статического момента МС в первом квадранте координатной плоскости, то зависимость динамического момента МД=f(ω) будет иметь вид, представленный на рисунке 1.8 (заштрихованная часть).
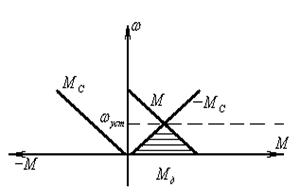При этом по мере увеличения угловой скорости вращения ω, динамический момент МД будет уменьшаться и при некоторой скорости ω=ωУСТ, динамический момент станет равным нулю.
Рисунок 1.8
Найдем динамический или избыточный момент: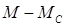 
.
Поставим перед собой задачу, используя характеристики, записать дифференциальные уравнения. Соответственно найдем их решение и построим динамические характеристики 
, представленные на рисунке 1.9.
|
|
|
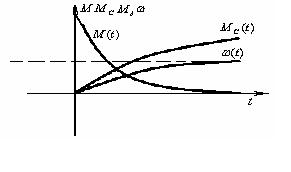Рисунок 1.9
2. Пусть в момент времени t=0 ЭП вращается с угловой скоростью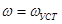 
под действием М и МС, представленных в предыдущем примере. Пусть в этот момент двигатель выключается из сети и при этом М=0 и на единичный элемент действует только МС. Тогда МД= - МС.
.
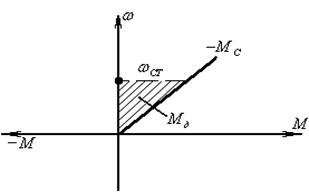
Рисунок 1.10
Записать дифференциальные уравнения и найти их решение. Динамические характеристики представлены на рисунке 1.11
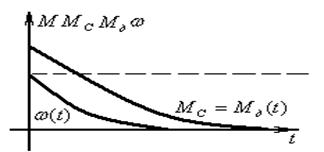
Рисунок 1.11
3. Ту же самую задачу решим при условии, что статический момент сопротивления постоянный.
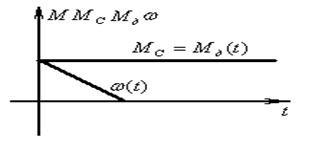
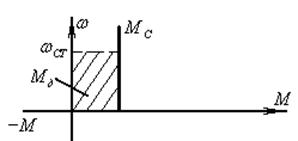
Рисунок 1.12
