Пусть эмпирическое распределение задано в виде последовательности интервалов 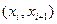 и соответствующих им частот
и соответствующих им частот 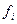 (
(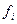 - сумма частот, которые попали в i – й интервал):
- сумма частот, которые попали в i – й интервал):
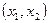 | 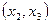 | … | 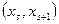 |
 |  | … | 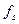 |
Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально.
Правило 2. Для того, чтобы при уровне значимости 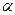 проверить гипотезу о нормальном распределении генеральной совокупности, надо:
проверить гипотезу о нормальном распределении генеральной совокупности, надо:
1. Вычислить, например методом произведений, выборочную среднюю 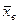 и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение 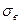 , причем в качестве вариант
, причем в качестве вариант 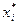 принимают среднее арифметическое концов интервала:
принимают среднее арифметическое концов интервала:
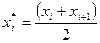 .
.
2. Пронормировать Х, т.е. перейти к случайной величине 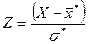 , и вычислить концы интервалов:
, и вычислить концы интервалов: 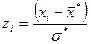 ,
, 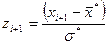 , причем наименьшее значение Z, т.е.
, причем наименьшее значение Z, т.е. 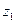 , полагают равным
, полагают равным 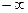 , а нибольшее, т.е.
, а нибольшее, т.е. 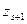 , полагают равным
, полагают равным 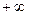 .
.
3. Вычислить теоретические частоты
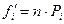 ,
,
где n – объем выборки (сумма всех частот); 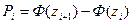 - вероятности попадания Х в интервалы
- вероятности попадания Х в интервалы 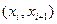 ;
; 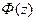 - функция Лапласа.
- функция Лапласа.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
а) составляют расчетную таблицу (см. выше), по которой находят наблюдаемое значение критерия Пирсона
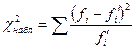 ;
;
б) по таблице критических точек распределения 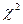 , по заданному уровню значимости
, по заданному уровню значимости 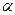 и числу степеней свободы
и числу степеней свободы 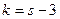 (s – число интервалов выборки) находят критическую точку правосторонней критической области
(s – число интервалов выборки) находят критическую точку правосторонней критической области  .
.
Если 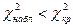 - нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Если
- нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Если  - гипотезу отвергают.
- гипотезу отвергают.
Замечание 2. Интервалы, содержащие малочисленные эмпирические частоты 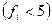 следует объединить, а частоты этих интервалов сложить. Если производилось объединение интервалов, то при определении числа степеней свободы по формуле
следует объединить, а частоты этих интервалов сложить. Если производилось объединение интервалов, то при определении числа степеней свободы по формуле 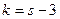 следует в качестве s принять число интервалов, оставшихся после объединения интервалов.
следует в качестве s принять число интервалов, оставшихся после объединения интервалов.
Гипотезу о нормальном распределении генеральной совокупности можно проверить графически методом спрямленных диаграмм. Этот материал следует рассмотреть самостоятельно (стр. 259 В.Е. Гмурман "Руководство к решению задач по теории вероятностей и математической статистике").
 2014-02-09
2014-02-09 1776
1776